الكسيريات هي أنماط لا نهائية تم إنشاؤها بواسطة تكرار المعادلات الرياضية. سنقوم برسم واحدة من أشهر الكسيريات، باستخدام فقط جافا سكريبت الأساسي وواجهة برمجة تطبيقات HTML5 Canvas.الكسيريات هي أنماط لا نهائية تم إنشاؤها بواسطة تكرار المعادلات الرياضية. سنقوم برسم واحدة من أشهر الكسيريات، باستخدام فقط جافا سكريبت الأساسي وواجهة برمجة تطبيقات HTML5 Canvas.

برمجة شجرة كسورية باستخدام جافا سكريبت وHTML5

بواسطة: Hackernoon

2025/10/11 03:00

TREE$0.1697-27.97%

LL$0.009119-5.93%

\ الكسيريات، تلك الأشكال الغامضة الموجودة في كل مكان ولكن لا يمكن رؤيتها بالعين غير المدربة. اليوم سنرسم واحدة من أشهر الكسيريات، باستخدام فقط Vanilla JS و HTML5 Canvas API. هيا بنا نبدأ البرمجة!

ما الذي ستتعلمه

ما هي شجرة الكسيريات؟
كتابة شجرة الكسيريات بلغة Vanilla JS
ما بعد شجرة الكسيريات

ما هي شجرة الكسيريات؟

لتعريف شجرة الكسيريات، أولاً، يجب أن نعرف تعريف الكسيريات، بالطبع.

الكسيريات هي أنماط لا نهائية تم إنشاؤها بتكرار المعادلات الرياضية، والتي على أي مقياس، وعلى أي مستوى من التكبير، تبدو متشابهة تقريبًا. بعبارة أخرى، كائن هندسي تتكرر بنيته الأساسية، الخشنة أو المجزأة، في مقاييس مختلفة.

لذلك إذا قسمنا الكسيريات، سنرى نسخة مصغرة من الكل.

قال بينوا ماندلبروت، الذي صاغ مصطلح الكسيريات في عام 1975:

\ واضح تمامًا، أليس كذلك؟

إليك بعض الأمثلة:

Animated Von Koch Curve

\ Animated Sierpinski Carpet

الآن، ما هي شجرة الكسيريات؟

تخيل فرعًا، وفروعًا تخرج منه، ثم فرعين يخرجان من كل فرع، وهكذا... هذا هو شكل شجرة الكسيريات.

يأتي شكلها من مثلث سيربينسكي (أو حشية سيربينسكي).

كما ترى، يتحول أحدهما إلى الآخر عند تغيير الزاوية بين الفروع:

From Sierpinski Triangle to Fractal

اليوم، سننتهي بشكل مشابه للشكل النهائي لتلك الصورة المتحركة.

كتابة شجرة الكسيريات بلغة Vanilla JS

أولاً وقبل كل شيء، إليك المنتج النهائي (يمكنك تعديله على طول الطريق):

Final Fractal Tree

الآن دعنا نرسم ذلك، خطوة بخطوة.

أولاً وقبل كل شيء، نقوم بتهيئة ملف index.html الخاص بنا بلوحة قماش ذات أبعاد معقولة وعلامة نصية حيث ستكون جميع أكواد JS الخاصة بنا.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

ثم، نبدأ في كتابة JavaScript الخاص بنا.

نقوم بتهيئة عنصر اللوحة على JS، من خلال الوصول إليه عبر متغير myCanvas وإنشاء سياق العرض ثنائي الأبعاد باستخدام متغير ctx (السياق).

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

نعم، طريقة getContext تضيف خصائص وطرق تسمح لك بالرسم، في هذه الحالة، في الأبعاد الثنائية.

الآن حان وقت التفكير. كيف يمكننا تحديد الخوارزمية لرسم شجرة الكسيريات؟ هم... 🤔

دعنا نرى، نحن نعلم أن الفروع تستمر في أن تصبح أصغر. وأن كل فرع ينتهي بفرعين يخرجان منه، واحد إلى اليسار وواحد إلى اليمين.

بعبارة أخرى، عندما يكون الفرع طويلاً بما فيه الكفاية، قم بإرفاق فرعين أصغر به. كرر.

يبدو كما لو أننا يجب أن نستخدم بعض العبارات التكرارية في مكان ما، أليس كذلك؟

بالعودة إلى الكود، نحدد الآن وظيفتنا fractalTree التي يجب أن تأخذ على الأقل أربع وسائط: إحداثيات X و Y حيث يبدأ الفرع، وطول فرعه، وزاويته.

داخل وظيفتنا، نبدأ الرسم بطريقة beginPath()، ثم نحفظ حالة اللوحة بطريقة save().

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

غالبًا ما يتم استخدام طريقة beginPath عندما تبدأ خطًا أو شكلًا جديدًا له نمط ثابت، مثل نفس اللون على طول الخط بأكمله، أو نفس العرض. طريقة save تحفظ فقط الحالة الكاملة للوحة عن طريق دفع الحالة الحالية إلى مكدس.

الآن سنرسم شجرة الكسيريات الخاصة بنا عن طريق رسم خط (فرع)، وتدوير اللوحة، ورسم الفرع التالي، وهكذا. يسير الأمر على هذا النحو (سأشرح كل طريقة أدناه عينة الكود):

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

لذلك نضيف أولاً ثلاث طرق، translate و rotate و moveTo، والتي "تحرك" اللوحة وأصلها و "قلمنا" حتى نتمكن من رسم الفرع بالزاوية التي نريدها. إنه كما لو كنا نرسم فرعًا، ثم نقوم بتوسيط هذا الفرع (عن طريق تحريك اللوحة بأكملها)، ثم نرسم فرعًا جديدًا من نهاية فرعنا السابق.

الطريقتان الأخيرتان قبل عبارة if هما lineTo و stroke؛ الأولى تضيف خطًا مستقيمًا إلى المسار الحالي، والثانية تعرضه. يمكنك التفكير في الأمر على هذا النحو: lineTo تعطي الأمر، و stroke تنفذه.

الآن لدينا عبارة if تخبرنا متى نتوقف عن التكرار، متى نتوقف عن الرسم. طريقة restore، كما هو مذكور في وثائق MDN، "تستعيد حالة اللوحة المحفوظة مؤخرًا عن طريق إخراج الإدخال العلوي في مكدس حالة الرسم".

بعد عبارة if، لدينا استدعاء تكراري واستدعاء آخر لطريقة restore. ثم استدعاء للوظيفة التي انتهينا للتو منها.

الآن قم بتشغيل الكود في متصفحك. سترى، أخيرًا، شجرة الكسيريات!

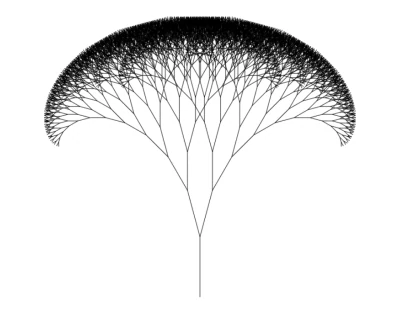
Fractal Tree First Iteration

رائع، أليس كذلك؟ الآن دعنا نجعلها أفضل.

سنضيف معلمة جديدة إلى وظيفة الرسم الخاصة بنا، branchWidth، لجعل شجرة الكسيريات الخاصة بنا أكثر واقعية.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

لذلك في كل تكرار، نجعل كل فرع أرفع. لقد غيرت أيضًا معلمة الزاوية في الاستد

إخلاء مسؤولية: المقالات المُعاد نشرها على هذا الموقع مستقاة من منصات عامة، وهي مُقدمة لأغراض إعلامية فقط. لا تُظهِر بالضرورة آراء MEXC. جميع الحقوق محفوظة لمؤلفيها الأصليين. إذا كنت تعتقد أن أي محتوى ينتهك حقوق جهات خارجية، يُرجى التواصل عبر البريد الإلكتروني service@support.mexc.com لإزالته. لا تقدم MEXC أي ضمانات بشأن دقة المحتوى أو اكتماله أو حداثته، وليست مسؤولة عن أي إجراءات تُتخذ بناءً على المعلومات المُقدمة. لا يُمثل المحتوى نصيحة مالية أو قانونية أو مهنية أخرى، ولا يُعتبر توصية أو تأييدًا من MEXC.

مشاركة الرؤى