Por qué los investigadores de IA están hablando sobre el Entrenamiento Espectral Disperso

Tabla de Enlaces

Abstracto y 1. Introducción

1. Trabajo Relacionado

2. Adaptación de Rango Bajo

   3.1 LoRA y 3.2 Limitación de LoRA

   3.3 ReLoRA*

3. Entrenamiento Espectral Disperso

   4.1 Preliminares y 4.2 Actualización de Gradiente de U, VT con Σ

   4.3 Por qué la Inicialización SVD es Importante

   4.4 SST Equilibra Explotación y Exploración

   4.5 Implementación Eficiente en Memoria para SST y 4.6 Dispersión de SST

4. Experimentos

   5.1 Traducción Automática

   5.2 Generación de Lenguaje Natural

   5.3 Redes Neuronales Hiperbólicas de Grafos

5. Conclusión y Discusión

6. Impactos Más Amplios y Referencias

Información Suplementaria

A. Algoritmo de Entrenamiento Espectral Disperso

B. Demostración del Gradiente de la Capa Espectral Dispersa

C. Demostración de la Descomposición del Gradiente del Peso

D. Demostración de la Ventaja del Gradiente Mejorado sobre el Gradiente Predeterminado

E. Demostración de Distorsión Cero con Inicialización SVD

F. Detalles del Experimento

G. Poda de Valores Singulares

H. Evaluación de SST y GaLore: Enfoques Complementarios para la Eficiencia de Memoria

I. Estudio de Ablación

A Algoritmo de Entrenamiento Espectral Disperso

B Demostración del Gradiente de la Capa Espectral Dispersa

Podemos expresar el diferencial de W como la suma de diferenciales:

\ \

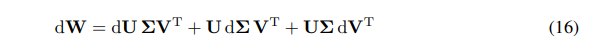
\ \ Tenemos la regla de la cadena para el gradiente de W:

\ \

\ \ \

\

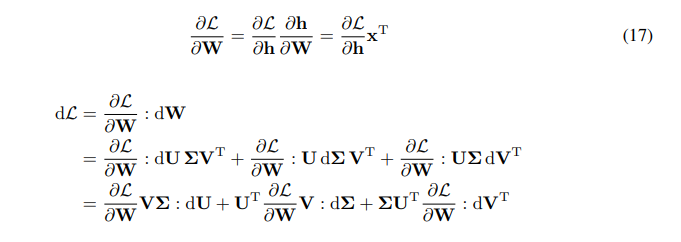
C Demostración de la Descomposición del Gradiente del Peso

\

\

D Demostración de la Ventaja del Gradiente Mejorado sobre el Gradiente Predeterminado

\

\ \ \

\ \ \

\ \ Como solo importa la dirección de la actualización, la escala de actualización puede ajustarse cambiando la tasa de aprendizaje. Medimos la similitud utilizando la norma de Frobenius de las diferencias entre las actualizaciones SST y 3 veces la actualización de rango completo.

\ \

\

E Demostración de Distorsión Cero con Inicialización SVD

\

F Detalles del Experimento

F.1 Detalles de Implementación para SST

\

\ \ \

\

F.2 Hiperparámetros de Traducción Automática

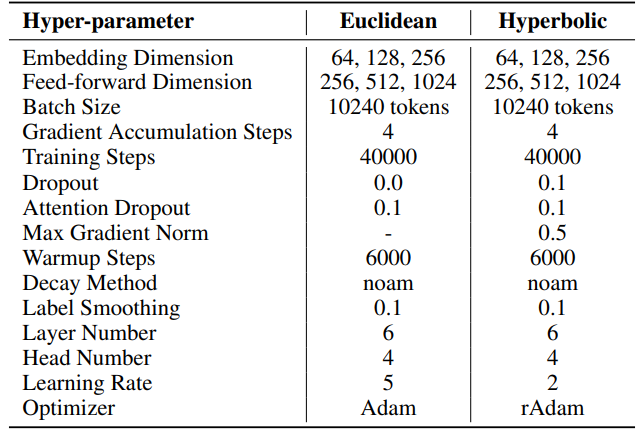
IWSLT'14. Los hiperparámetros se pueden encontrar en la Tabla 6. Empleamos la misma base de código e hiperparámetros que los utilizados en HyboNet [12], que se deriva de OpenNMT-py [54]. El punto de control final del modelo se utiliza para la evaluación. La búsqueda de haz, con un tamaño de haz de 2, se emplea para optimizar el proceso de evaluación. Los experimentos se realizaron en una GPU A100.

\ Para SST, el número de pasos por iteración (T3) se establece en 200. Cada iteración comienza con una fase de calentamiento que dura 20 pasos. El número de iteraciones por ronda (T2) se determina mediante la fórmula T2 = d/r, donde d representa la dimensión de incrustación y r denota el rango utilizado en SST.

\ \

\ \ \

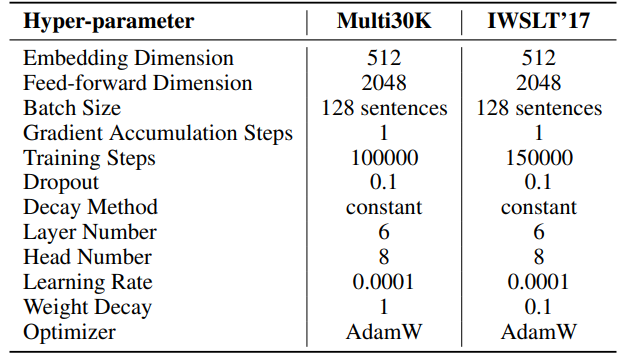
\ \ Para SST, el número de pasos por iteración (T3) se establece en 200 para Multi30K y 400 para IWSLT'17. Cada iteración comienza con una fase de calentamiento que dura 20 pasos. El número de iteraciones por ronda (T2) se determina mediante la fórmula T2 = d/r, donde d representa la dimensión de incrustación y r denota el rango utilizado en SST

F.3 Hiperparámetros de Generación de Lenguaje Natural

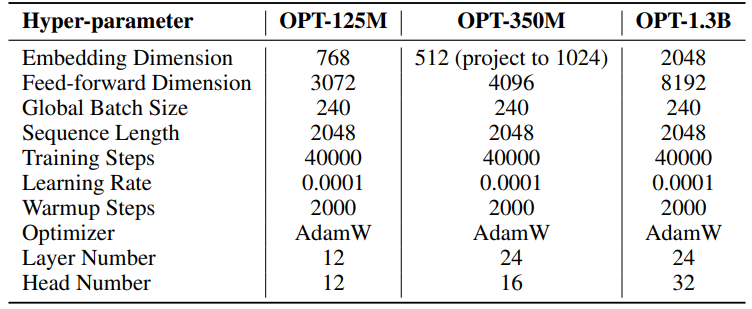
Los hiperparámetros para nuestros experimentos se detallan en la Tabla 8. Empleamos un calentamiento lineal de 2000 pasos seguido de una tasa de aprendizaje estable, sin decaimiento. Se utiliza una tasa de aprendizaje mayor (0.001) solo para parámetros de bajo rango (U, VT y Σ para SST, B y A para LoRA y ReLoRA*. El total de tokens de entrenamiento para cada experimento es 19.7B, aproximadamente 2 épocas de OpenWebText. El entrenamiento distribuido se facilita utilizando la biblioteca Accelerate [55] en cuatro GPUs A100 en un servidor Linux.

\ Para SST, el número de pasos por iteración (T3) se establece en 200. Cada iteración comienza con una fase de calentamiento que dura 20 pasos. El número de iteraciones por ronda (T2) se determina mediante la fórmula T2 = d/r, donde d representa la dimensión de incrustación y r denota el rango utilizado en SST.

\ \

\ \ \

\

F.4 Hiperparámetros de Redes Neuronales Hiperbólicas de Grafos

Utilizamos HyboNet [12] como modelo de rango completo, con los mismos hiperparámetros que los utilizados en HyboNet. Los experimentos se realizaron en una GPU A100.

\ Para SST, el número de pasos por iteración (T3) se establece en 100. Cada iteración comienza con una fase de calentamiento que dura 100 pasos. El número de iteraciones por ronda (T2) se determina mediante la fórmula T2 = d/r, donde d representa la dimensión de incrustación y r denota el rango utilizado en SST.

\ Establecemos la tasa de dropout en 0.5 para los métodos LoRA y SST durante la tarea de clasificación de nodos en el conjunto de datos Cora. Esta es la única desviación de la configuración de HyboNet.

\ \ \

:::info Autores:

(1) Jialin Zhao, Centro de Inteligencia de Redes Complejas (CCNI), Laboratorio de Cerebro e Inteligencia de Tsinghua (THBI) y Departamento de Ciencias de la Computación;

(2) Yingtao Zhang, Centro de Inteligencia de Redes Complejas (CCNI), Laboratorio de Cerebro e Inteligencia de Tsinghua (THBI) y Departamento de Ciencias de la Computación;

(3) Xinghang Li, Departamento de Ciencias de la Computación;

(4) Huaping Liu, Departamento de Ciencias de la Computación;

(5) Carlo Vittorio Cannistraci, Centro de Inteligencia de Redes Complejas (CCNI), Laboratorio de Cerebro e Inteligencia de Tsinghua (THBI), Departamento de Ciencias de la Computación y Departamento de Ingeniería Biomédica de la Universidad de Tsinghua, Beijing, China.

:::

:::info Este artículo está disponible en arxiv bajo la licencia CC by 4.0 Deed (Atribución 4.0 Internacional).

:::

\