Cómo la Mezcla de Adaptaciones Hace que el Ajuste Fino de Modelos de Lenguaje sea Más Económico e Inteligente

Tabla de Enlaces

Abstracto y 1. Introducción

1. Antecedentes

   2.1 Mezcla de Expertos

   2.2 Adaptadores

2. Mezcla de Adaptaciones

   3.1 Política de Enrutamiento

   3.2 Regularización de consistencia

   3.3 Fusión de módulos de adaptación y 3.4 Compartición de módulos de adaptación

   3.5 Conexión con Redes Neuronales Bayesianas y Ensamblaje de Modelos

3. Experimentos

   4.1 Configuración Experimental

   4.2 Resultados Clave

   4.3 Estudio de Ablación

4. Trabajo Relacionado

5. Conclusiones

6. Limitaciones

7. Agradecimientos y Referencias

Apéndice

A. Conjuntos de datos NLU de pocos ejemplos B. Estudio de Ablación C. Resultados Detallados en Tareas NLU D. Hiperparámetro

3 Mezcla de Adaptaciones

\

3.1 Política de Enrutamiento

Trabajos recientes como THOR (Zuo et al., 2021) han demostrado que la política de enrutamiento estocástico como el enrutamiento aleatorio funciona tan bien como el mecanismo de enrutamiento clásico como el enrutamiento Switch (Fedus et al., 2021) con los siguientes beneficios. Dado que los ejemplos de entrada se enrutan aleatoriamente a diferentes expertos, no hay requisito para equilibrio de carga adicional ya que cada experto tiene la misma oportunidad de ser activado simplificando el marco. Además, no hay parámetros adicionales, y por lo tanto no hay cálculo adicional, en la capa Switch para la selección de expertos. Esto último es particularmente importante en nuestro entorno para el ajuste fino eficiente en parámetros para mantener los parámetros y FLOPs iguales a los de un solo módulo de adaptación. Para analizar el funcionamiento de AdaMix, demostramos conexiones al enrutamiento estocástico y al promedio de pesos del modelo con Redes Neuronales Bayesianas y ensamblaje de modelos en la Sección 3.5.

\ \

\ \ Este enrutamiento estocástico permite que los módulos de adaptación aprendan diferentes transformaciones durante el entrenamiento y obtengan múltiples vistas de la tarea. Sin embargo, esto también crea un desafío sobre qué módulos usar durante la inferencia debido al protocolo de enrutamiento aleatorio durante el entrenamiento. Abordamos este desafío con las siguientes dos técnicas que además nos permiten colapsar módulos de adaptación y obtener el mismo costo computacional (FLOPs, #parámetros de adaptación ajustables) que el de un solo módulo.

3.2 Regularización de consistencia

\

\ \ \

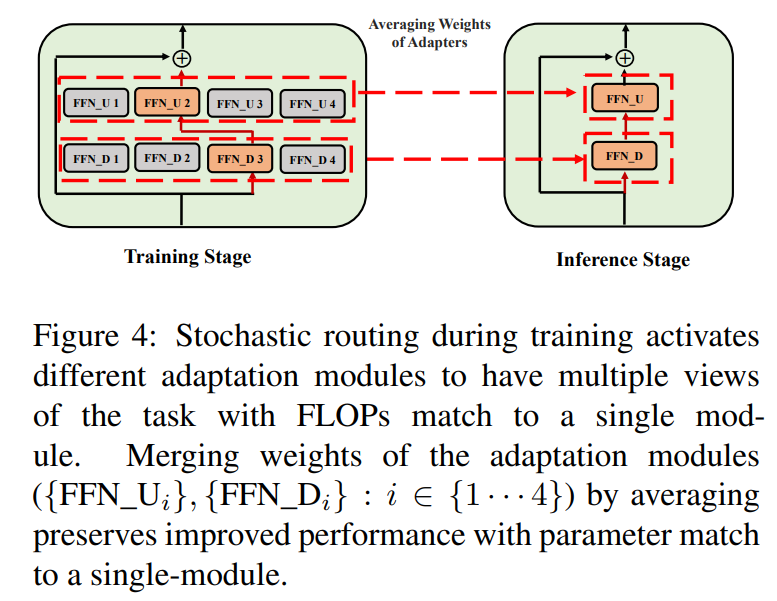
3.3 Fusión de módulos de adaptación

Si bien la regularización anterior mitiga la inconsistencia en la selección aleatoria de módulos durante la inferencia, todavía resulta en un mayor costo de servicio para alojar varios módulos de adaptación. Trabajos anteriores en el ajuste fino de modelos de lenguaje para tareas posteriores han mostrado un rendimiento mejorado al promediar los pesos de diferentes modelos ajustados con diferentes semillas aleatorias superando a un solo modelo ajustado. Trabajos recientes (Wortsman et al., 2022) también han demostrado que los modelos ajustados de manera diferente desde la misma inicialización se encuentran en la misma cuenca de error, motivando el uso de la agregación de pesos para una robusta síntesis de tareas. Adoptamos y extendemos técnicas previas para el ajuste fino de modelos de lenguaje a nuestro entrenamiento eficiente en parámetros de módulos de adaptación de múltiples vistas

\ \

\

3.4 Compartición de módulos de adaptación

\

3.5 Conexión con Redes Neuronales Bayesianas y Ensamblaje de Modelos

\

\ \ Esto requiere promediar sobre todos los pesos de modelo posibles, lo cual es intratable en la práctica. Por lo tanto, se han desarrollado varios métodos de aproximación basados en métodos de inferencia variacional y técnicas de regularización estocástica utilizando dropouts. En este trabajo, aprovechamos otra regularización estocástica en forma de enrutamiento aleatorio. Aquí, el objetivo es encontrar una distribución sustituta qθ(w) en una familia tratable de distribuciones que pueda reemplazar la posterior del modelo verdadero que es difícil de calcular. El sustituto ideal se identifica minimizando la divergencia de Kullback-Leibler (KL) entre el candidato y la posterior verdadera.

\ \

\ \ \

\ \ \

\ \ \ \

:::info Autores:

(1) Yaqing Wang, Purdue University (wang5075@purdue.edu);

(2) Sahaj Agarwal, Microsoft (sahagar@microsoft.com);

(3) Subhabrata Mukherjee, Microsoft Research (submukhe@microsoft.com);

(4) Xiaodong Liu, Microsoft Research (xiaodl@microsoft.com);

(5) Jing Gao, Purdue University (jinggao@purdue.edu);

(6) Ahmed Hassan Awadallah, Microsoft Research (hassanam@microsoft.com);

(7) Jianfeng Gao, Microsoft Research (jfgao@microsoft.com).

:::

:::info Este artículo está disponible en arxiv bajo la licencia CC BY 4.0 DEED.

:::

\