No hay ganadores aquí: Por qué cada subasta "justa" de cripto termina siendo trivial

Tabla de enlaces

Abstracto y 1. Introducción

1.1 Visión técnica general

1.2 Trabajos relacionados

1. Modelo y preliminares y 2.1 Mecanismos de comisiones por transacción

   2.2 Los desiderata de TFM

2. Entendiendo OCA

   3.1 La diferencia entre SCP y OCA

   3.2 Resultados preliminares útiles para TFMs a prueba de OCA

3. Mecanismos determinísticos a prueba de OCA

4. Mecanismos aleatorizados a prueba de OCA

5. Discusión y Referencias

   \

A. Pruebas faltantes

B. Mecanismos determinísticos no anónimos

4 Mecanismos determinísticos a prueba de OCA

El ejemplo 3.6 muestra que, en general, las propiedades DSIC y 1-OCA-proofness no son suficientes para garantizar ingresos cero. Ahora mostramos que para mecanismos determinísticos, agregar la propiedad MMIC es suficiente para obtener un resultado general de ingresos 0.

\ Teorema 4.1. Cada mecanismo determinístico DSIC+MMIC+1-OCA-proof tiene 0 ingresos para el minero.

\

\ Sin embargo, podemos proporcionar una caracterización significativa incluso al eliminar la condición DSIC. La caracterización, dada en el Lema 4.3, sigue siendo muy similar, aunque con más libertad para decidir la regla de pago.

\

\ Concluimos que la quema para todos los valores asignados es alguna constante R. Ahora comparamos R con la r que tenemos para la regla de asignación.

\ Concluimos que R = r, lo que produce la caracterización especificada.

\ Esto nos permite caracterizar aún más las reglas de asignación y quema de manera más general, para mecanismos determinísticos 1-OCA-proof.

\ Lema 4.4. Cualquier mecanismo determinístico 1-OCA-proof a, p, β tiene exactamente la siguiente forma: Para algún r ≥ 0, el mecanismo asigna el artículo al mejor postor sujeto a que tenga un valor más alto que r, o no asigna el artículo en absoluto. Siempre que se asigne, la quema es exactamente r. Es decir,

\

\

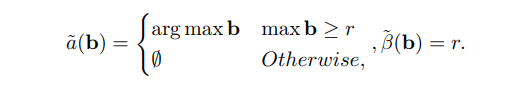
\ Ahora podemos caracterizar con precisión dos clases de mecanismos: La clase de mecanismos determinísticos DSIC+1-OCA-proof, y la clase de mecanismos determinísticos MMIC+1-OCA-proof.

\

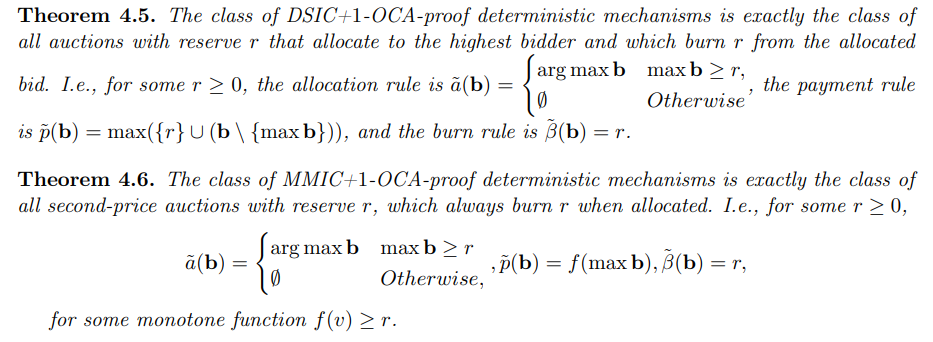
\ Estas caracterizaciones precisas ahora nos permiten concluir con lo siguiente:

Teorema 4.7. Nunca asignar el artículo es el único mecanismo determinístico DSIC+MMIC+1-OCA-proof.

\ Prueba. Esto se deduce del Teorema 4.5 y el Teorema 4.6, ya que las dos clases caracterizadas en estos resultados solo tienen el mecanismo trivial en común (tomando r = ∞). Para ver esto intuitivamente, considere la clase de subastas de segundo precio con reserva r y quema constante r del Teorema 4.5. Las subastas de segundo precio no son MMIC ya que el minero puede agregar un postor falso arbitrariamente cerca de la oferta ganadora para aumentar el pago.

\

5 Mecanismos aleatorizados a prueba de OCA

Ahora extendemos la discusión a mecanismos aleatorizados a prueba de OCA. Para mecanismos aleatorizados, consideramos la noción más fuerte de OCA-proofness (en lugar de 1-OCA-proofness). Lo hacemos para evitar el desorden en las definiciones, ya que en mecanismos aleatorizados, la coalición ganadora bien puede incluir necesariamente a todos los postores (ya que cada uno tiene alguna probabilidad fraccional de ganar).

\ Ahora consideramos una propiedad natural para los mecanismos:

\ Corolario 5.4. Por el Lema 5.3, un mecanismo invariante a escala DSIC+OCA-proof no quema comisiones (es decir, su regla de quema es la función constante cero), mientras que del Lema 3.5 obtenemos que un mecanismo DSIC+MMIC+OCAproof tiene pagos iguales a la quema en el caso de un solo postor. Por lo tanto, debemos tener 0 pagos en el caso de un solo postor, y así, en el caso de un solo postor, el artículo siempre se asigna o nunca se asigna.

\ Lema 5.5. Para un mecanismo DSIC+MMIC+OCA-proof, si el artículo siempre se asigna o nunca se asigna en el caso de un solo postor, el mecanismo debe ser trivial.

\

\ Así, como resultado directo del Corolario 5.4 y el Lema 5.5, tenemos:

Corolario 5.6. No existe un mecanismo no trivial invariante a escala DSIC+MMIC+OCA-proof.

\ El argumento que usamos en el Lema 5.5 puede extenderse para permitirnos también descartar la clase de subastas que satisfacen una propiedad que llamamos probabilidad total constante de asignación (CTPA), que se define en Def. 5.7. Esta es una clase interesante de subastas, ya que incluye todas las subastas eficientes (que son parte de la clase de probabilidad total constante 1 de asignación), incluidas las subastas de primer y segundo precio.

\

\

\

\ y así por la factibilidad Eq. (1):

\ Observe que este es el lado izquierdo del Lema 5.12 donde consideramos las ofertas B · b, A · b. Podemos así repetir la forma en que desarrollamos la Eq. (14) (para el caso de las ofertas A · b, A · b) y, considerando que el minero omite la oferta B · b, obtener:

\ Además, para el caso de dos postores, podemos mostrar un límite superior e inferior útil sobre cuánto debe "favorecer" la función al postor más alto:

\

\

\

\

:::info Autores:

(1) Yotam Gafni, Instituto Weizmann (yotam.gafni@gmail.com);

(2) Aviv Yaish, Universidad Hebrea, Jerusalén (aviv.yaish@mail.huji.ac.il).

:::

:::info Este artículo está disponible en arxiv bajo la licencia CC BY 4.0 DEED.

:::

\