Utilizamos conjuntos de datos tabulares originalmente de OpenML y compilados en un conjunto de datos de referencia del equipo Inria-Soda en HuggingFace. Entrenamos con 28.855 muestras de entrenamiento y probamos con las 9.619 muestras restantes. Todos los MLP se entrenan con un tamaño de lote de 64, 64 y 0,0005, y estudiamos 3 capas de 100 neuronas cada una. Definimos aquí las seis métricas principales utilizadas en nuestro trabajo.Utilizamos conjuntos de datos tabulares originalmente de OpenML y compilados en un conjunto de datos de referencia del equipo Inria-Soda en HuggingFace. Entrenamos con 28.855 muestras de entrenamiento y probamos con las 9.619 muestras restantes. Todos los MLP se entrenan con un tamaño de lote de 64, 64 y 0,0005, y estudiamos 3 capas de 100 neuronas cada una. Definimos aquí las seis métricas principales utilizadas en nuestro trabajo.

La Guía del Geek para la Experimentación con ML

Autor: Hackernoon

2025/09/21 13:47

Tabla de Enlaces

Abstracto y 1. Introducción

1.1 Explicación Post Hoc

1.2 El Problema de Desacuerdo

1.3 Fomentando el Consenso de Explicación

Trabajo Relacionado
Pear: Regularizador de Acuerdo de Explicador Post HOC
La Eficacia del Entrenamiento de Consenso

4.1 Métricas de Acuerdo

4.2 Mejorando las Métricas de Consenso

[4.3 ¿Consistencia a Qué Costo?]()

4.4 ¿Las Explicaciones Siguen Siendo Valiosas?

4.5 Consenso y Linealidad

4.6 Dos Términos de Pérdida
Discusión

5.1 Trabajo Futuro

5.2 Conclusión, Agradecimientos y Referencias

Apéndice

A APÉNDICE

A.1 Conjuntos de datos

En nuestros experimentos utilizamos conjuntos de datos tabulares originalmente de OpenML y compilados en un conjunto de conjuntos de datos de referencia del equipo Inria-Soda en HuggingFace [11]. Proporcionamos algunos detalles sobre cada conjunto de datos:

\ Bank Marketing Este es un conjunto de datos de clasificación binaria con seis características de entrada y está aproximadamente equilibrado en clases. Entrenamos con 7.933 muestras de entrenamiento y probamos con las 2.645 muestras restantes.

\ California Housing Este es un conjunto de datos de clasificación binaria con siete características de entrada y está aproximadamente equilibrado en clases. Entrenamos con 15.475 muestras de entrenamiento y probamos con las 5.159 muestras restantes.

\ Electricity Este es un conjunto de datos de clasificación binaria con siete características de entrada y está aproximadamente equilibrado en clases. Entrenamos con 28.855 muestras de entrenamiento y probamos con las 9.619 muestras restantes.

A.2 Hiperparámetros

Muchos de nuestros hiperparámetros son constantes en todos nuestros experimentos. Por ejemplo, todos los MLPs se entrenan con un tamaño de lote de 64 y una tasa de aprendizaje inicial de 0,0005. Además, todos los MLPs que estudiamos tienen 3 capas ocultas de 100 neuronas cada una. Siempre usamos el optimizador AdamW [19]. El número de épocas varía de un caso a otro. Para los tres conjuntos de datos, entrenamos durante 30 épocas cuando 𝜆 ∈ {0.0, 0.25} y 50 épocas en caso contrario. Al entrenar modelos lineales, usamos 10 épocas y una tasa de aprendizaje inicial de 0,1.

A.3 Métricas de Desacuerdo

Definimos cada una de las seis métricas de acuerdo utilizadas en nuestro trabajo aquí.

\ Las primeras cuatro métricas dependen de las características top-𝑘 más importantes en cada explicación. Sea 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) que representa las características top-𝑘 más importantes en una explicación 𝐸, sea 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) el rango de importancia de la característica 𝑠 dentro de la explicación 𝐸, y sea 𝑠𝑖𝑔𝑛(𝐸, 𝑠) el signo (positivo, negativo o cero) de la puntuación de importancia de la característica 𝑠 en la explicación 𝐸.

\ Las siguientes dos métricas de acuerdo dependen de todas las características dentro de cada explicación, no solo de las top-𝑘. Sea 𝑅 una función que calcula la clasificación de características dentro de una explicación por importancia.

\ (Nota: Krishna et al. [15] especifican en su artículo que 𝐹 debe ser un conjunto de características especificado por un usuario final, pero en nuestros experimentos usamos todas las características con esta métrica).

A.4 Resultados del Experimento con Características Basura

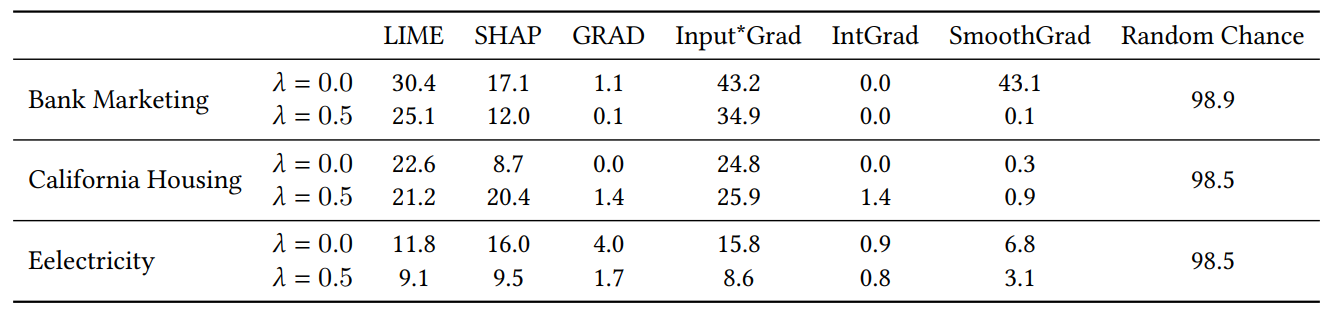
Cuando agregamos características aleatorias para el experimento en la Sección 4.4, duplicamos el número de características. Hacemos esto para comprobar si nuestra pérdida de consenso daña la calidad de la explicación al colocar características irrelevantes en el top-𝐾 con más frecuencia que los modelos entrenados naturalmente. En la Tabla 1, informamos el porcentaje de veces que cada explicador incluyó una de las características aleatorias en las 5 características más importantes. Observamos que en general, no vemos un aumento sistemático de estos porcentajes entre 𝜆 = 0.0 (un MLP de referencia sin nuestra pérdida de consenso) y 𝜆 = 0.5 (un MLP entrenado con nuestra pérdida de consenso)

\ Tabla 1: Frecuencia de características basura que obtienen clasificaciones top-5, medida en porcentaje.

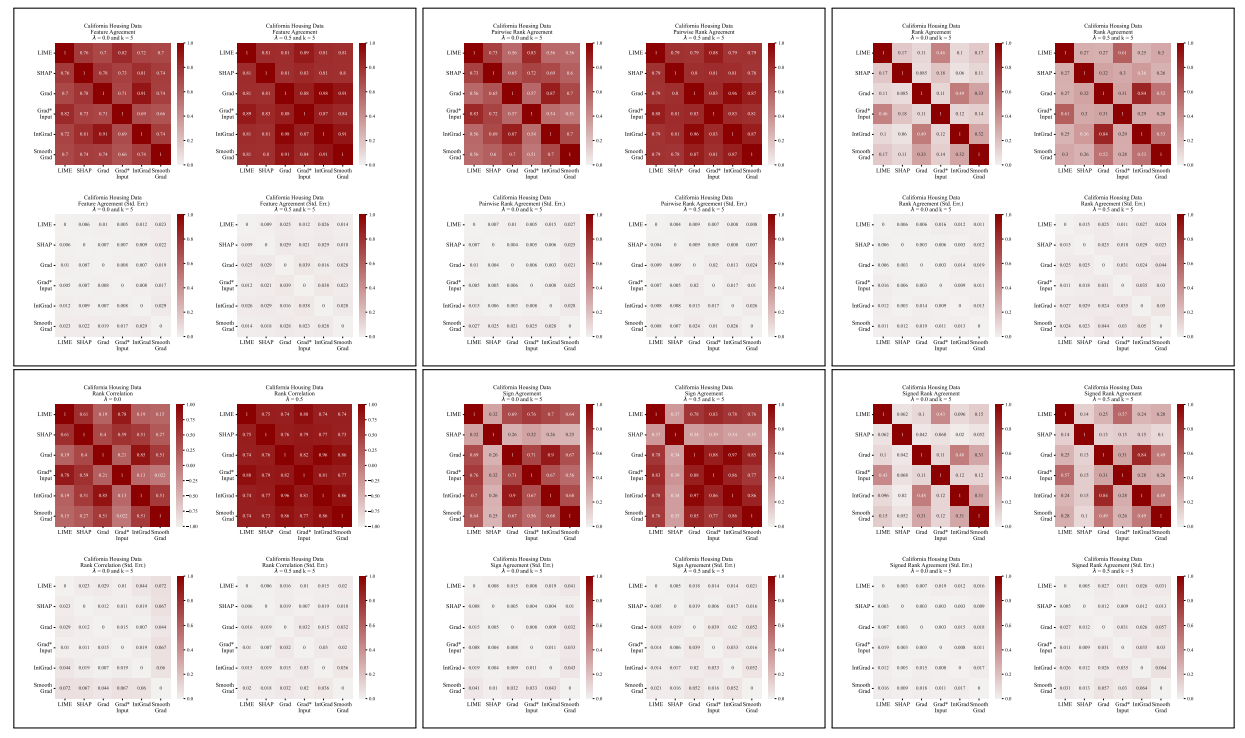
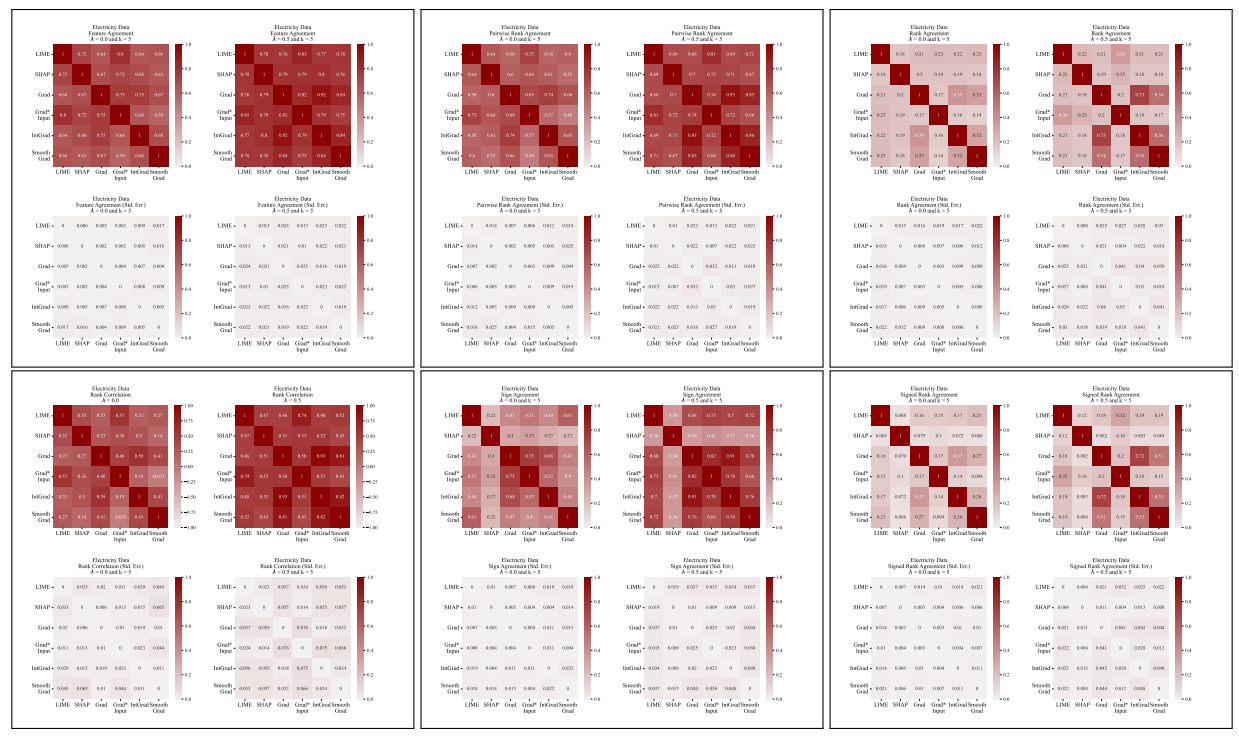
A.5 Más Matrices de Desacuerdo

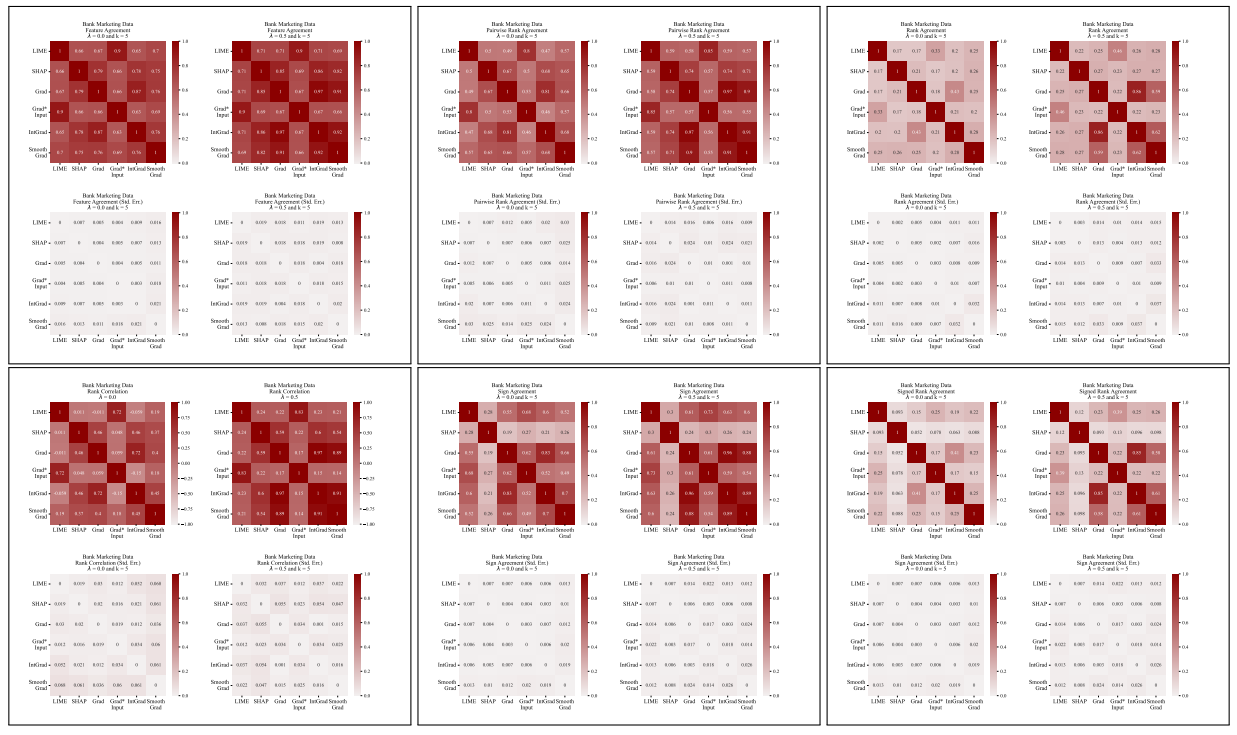
Figura 9: Matrices de desacuerdo para todas las métricas consideradas en este artículo sobre datos de Bank Marketing.

\ Figura 10: Matrices de desacuerdo para todas las métricas consideradas en este artículo sobre datos de California Housing.

\ Figura 11: Matrices de desacuerdo para todas las métricas consideradas en este artículo sobre datos de Electricity.

A.6 Resultados Extendidos

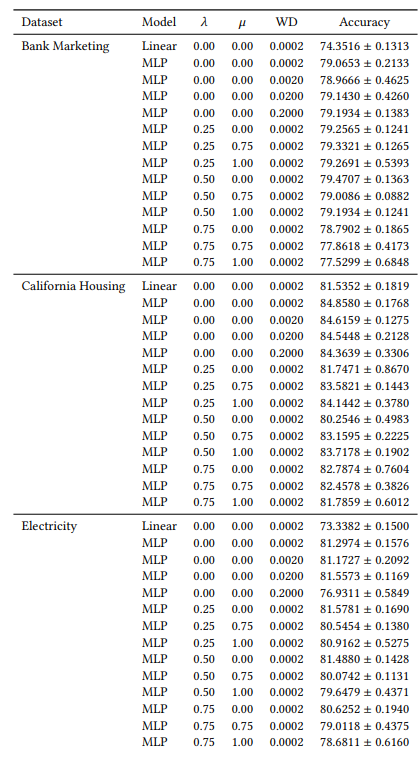
Tabla 2: Precisión media de prueba para los modelos que entrenamos. Esta tabla está organizada por conjunto de datos, modelo, los hiperparámetros en la pérdida y el coeficiente de decaimiento de peso (WD). Los promedios son sobre varios ensayos y reportamos las medias ± un error estándar.

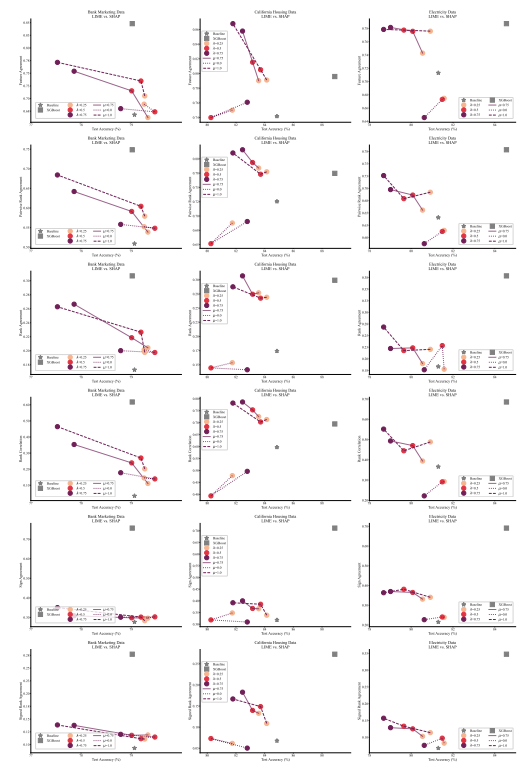
A.7 Gráficos Adicionales

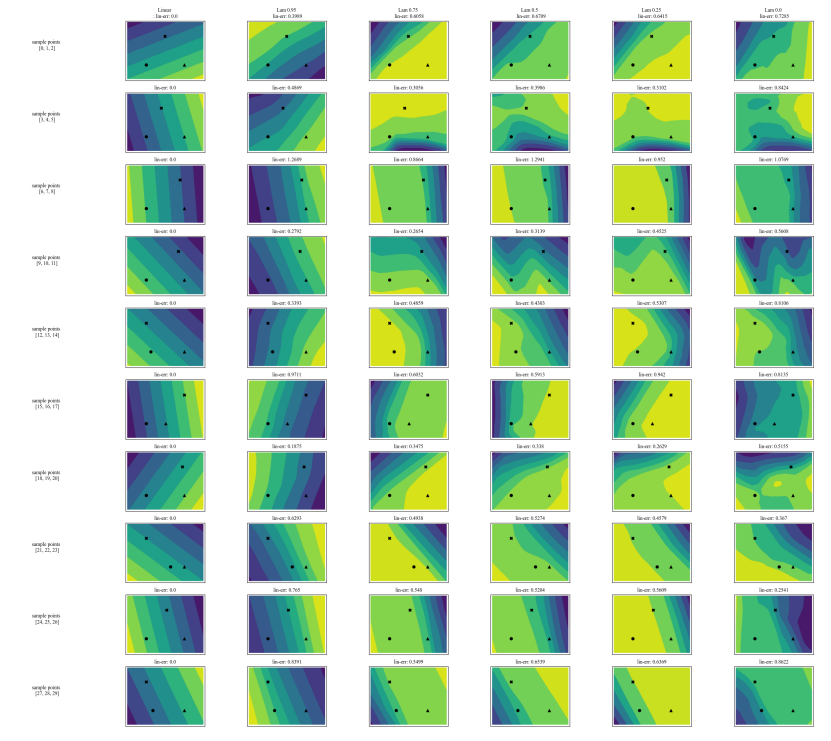
Figura 12: Las superficies logit para MLPs, cada una entrenada con un valor lambda diferente, en 10 planos de tres puntos construidos aleatoriamente del conjunto de datos Bank Marketing.

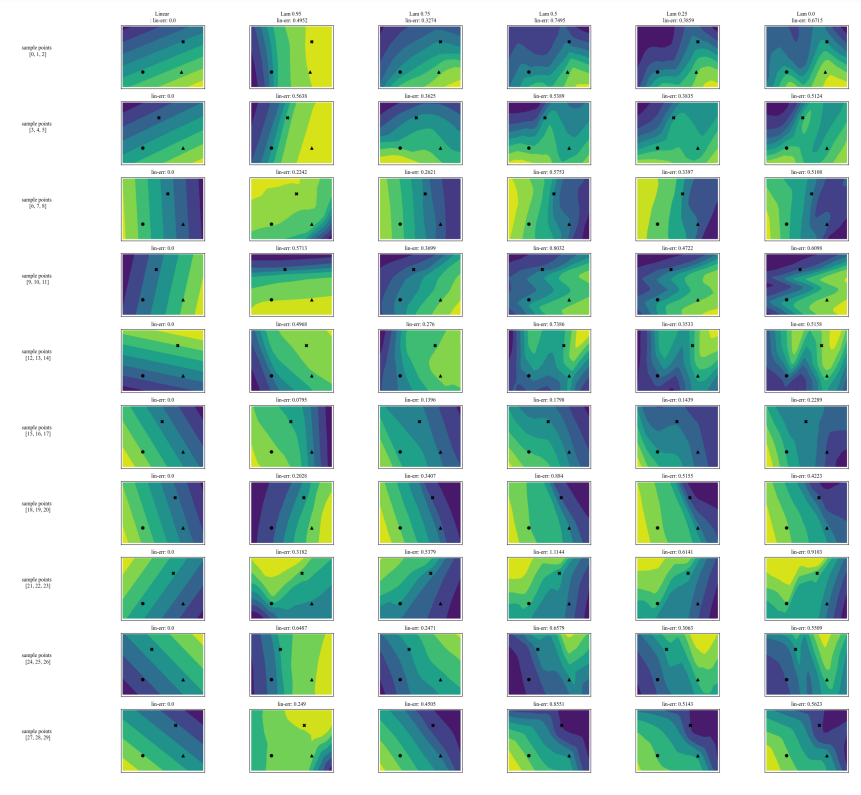
\ Figura 13: Las superficies logit para MLPs, cada una entrenada con un valor lambda diferente, en 10 planos de tres puntos construidos aleatoriamente del conjunto de datos California Housing.

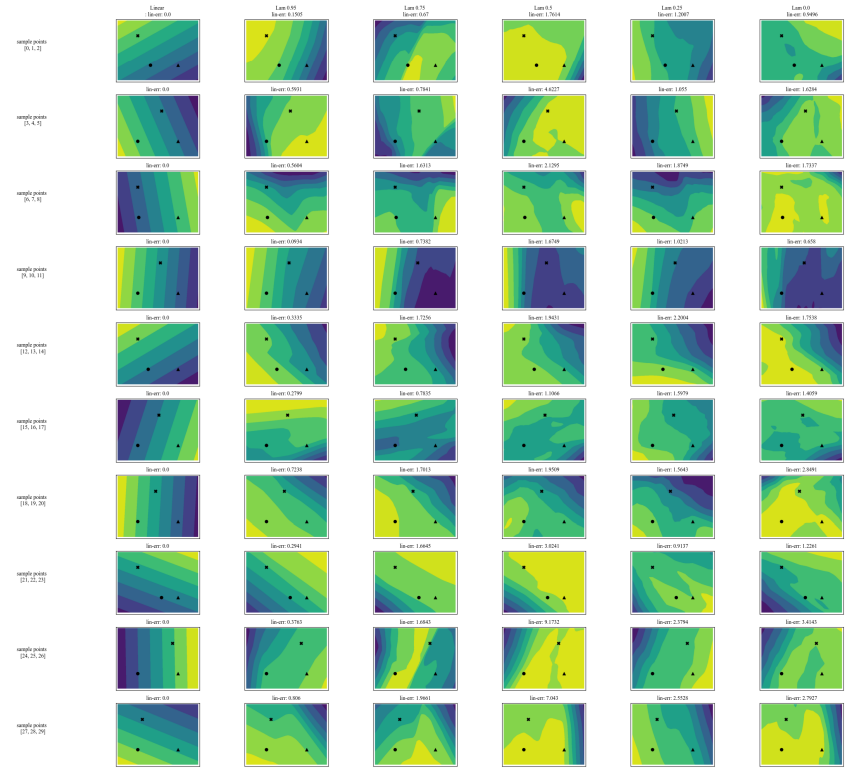
\ Figura 14: Las superficies logit para MLPs, cada una entrenada con un valor lambda diferente, en 10 planos de tres puntos construidos aleatoriamente del conjunto de datos Electricity.

\ Figura 15: Gráficos adicionales de curvas de compensación para todos los conjuntos de datos y métricas.

:::info Autores:

(1) Avi Schwarzschild, Universidad de Maryland, College Park, Maryland, EE.UU. y Trabajo completado mientras trabajaba en Arthur (avi1umd.edu);

(2) Max Cembalest, Arthur, Nueva York, Nueva York, EE.UU.;

(3) Karthik Rao, Arthur, Nueva York, Nueva York, EE.UU.;

(4) Keegan Hines, Arthur, Nueva York, Nueva York, EE.UU.;

(5) John Dickerson†, Arthur, Nueva York, Nueva York, EE.UU. (john@arthur.ai).

:::

:::info Este artículo está disponible en arxiv bajo la licencia CC BY 4.0 DEED.

:::

Aviso legal: Los artículos republicados en este sitio provienen de plataformas públicas y se ofrecen únicamente con fines informativos. No reflejan necesariamente la opinión de MEXC. Todos los derechos pertenecen a los autores originales. Si consideras que algún contenido infringe derechos de terceros, comunícate con service@support.mexc.com para solicitar su eliminación. MEXC no garantiza la exactitud, la integridad ni la actualidad del contenido y no se responsabiliza por acciones tomadas en función de la información proporcionada. El contenido no constituye asesoría financiera, legal ni profesional, ni debe interpretarse como recomendación o respaldo por parte de MEXC.

Compartir perspectivas