L'Entraînement Spectral Clairsemé (SST) introduit un cadre mathématiquement fondé pour optimiser les réseaux neuronaux en utilisant des décompositions spectrales de faible rang. En se concentrant sur la direction du gradient plutôt que sur l'échelle, SST réduit la charge de calcul tout en maintenant la stabilité d'apprentissage. L'article prouve une distorsion nulle avec l'initialisation SVD et une performance de gradient améliorée par rapport aux méthodes par défaut comme LoRA et HyboNet. Des expériences approfondies sur la traduction, la génération de langage et les réseaux neuronaux de graphes démontrent l'efficacité et la précision de SST, montrant sa promesse comme alternative évolutive à l'entraînement de rang complet.L'Entraînement Spectral Clairsemé (SST) introduit un cadre mathématiquement fondé pour optimiser les réseaux neuronaux en utilisant des décompositions spectrales de faible rang. En se concentrant sur la direction du gradient plutôt que sur l'échelle, SST réduit la charge de calcul tout en maintenant la stabilité d'apprentissage. L'article prouve une distorsion nulle avec l'initialisation SVD et une performance de gradient améliorée par rapport aux méthodes par défaut comme LoRA et HyboNet. Des expériences approfondies sur la traduction, la génération de langage et les réseaux neuronaux de graphes démontrent l'efficacité et la précision de SST, montrant sa promesse comme alternative évolutive à l'entraînement de rang complet.

Voici pourquoi les chercheurs en IA parlent de l'entraînement spectral clairsemé

Par : Hackernoon

2025/10/30 18:12

HERE$0.00012-24.52%

WHY$0.0000000248-2.63%

AI$0.06828-10.35%

ZERO$0.00001431-3.76%

LIKE$0.005575-8.27%

Table des Liens

Abstrait et 1. Introduction

Travaux Connexes
Adaptation de Rang Faible

3.1 LoRA et 3.2 Limitation de LoRA

3.3 ReLoRA*
Entraînement Spectral Sparse

4.1 Préliminaires et 4.2 Mise à jour du gradient de U, VT avec Σ

4.3 Pourquoi l'initialisation SVD est importante

4.4 SST équilibre exploitation et exploration

4.5 Implémentation économe en mémoire pour SST et 4.6 Sparsité de SST
Expériences

5.1 Traduction automatique

5.2 Génération de langage naturel

5.3 Réseaux de neurones graphiques hyperboliques
Conclusion et Discussion
Impacts plus larges et Références

Informations Supplémentaires

A. Algorithme d'Entraînement Spectral Sparse

B. Preuve du Gradient de la Couche Spectrale Sparse

C. Preuve de la Décomposition du Gradient du Poids

D. Preuve de l'Avantage du Gradient Amélioré sur le Gradient par Défaut

E. Preuve de Distorsion Zéro avec Initialisation SVD

F. Détails des Expériences

G. Élagage des Valeurs Singulières

H. Évaluation de SST et GaLore : Approches Complémentaires pour l'Efficacité de la Mémoire

I. Étude d'Ablation

A Algorithme d'Entraînement Spectral Sparse

B Preuve du Gradient de la Couche Spectrale Sparse

Nous pouvons exprimer le différentiel de W comme la somme des différentiels :

\ \

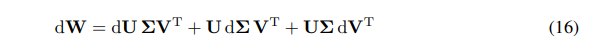
\ \ Nous avons la règle de chaîne pour le gradient de W :

\ \

\ \ \

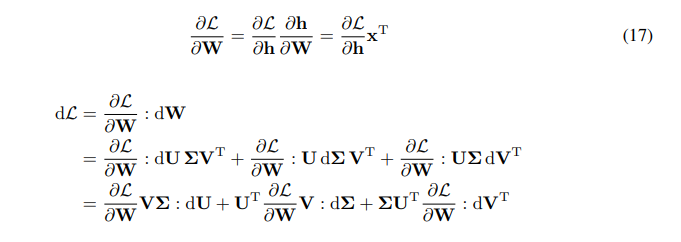
C Preuve de la Décomposition du Gradient du Poids

D Preuve de l'Avantage du Gradient Amélioré sur le Gradient par Défaut

\ \ \

\ \ Comme seule la direction de la mise à jour compte, l'échelle de la mise à jour peut être ajustée en modifiant le taux d'apprentissage. Nous mesurons la similarité en utilisant la norme de Frobenius des différences entre les mises à jour SST et 3 fois la mise à jour de rang complet.

\ \

E Preuve de Distorsion Zéro avec Initialisation SVD

F Détails des Expériences

F.1 Détails d'Implémentation pour SST

\ \ \

F.2 Hyperparamètres de la Traduction Automatique

IWSLT'14. Les hyperparamètres se trouvent dans le Tableau 6. Nous utilisons la même base de code et les mêmes hyperparamètres que ceux utilisés dans HyboNet [12], qui est dérivé d'OpenNMT-py [54]. Le point de contrôle final du modèle est utilisé pour l'évaluation. La recherche en faisceau, avec une taille de faisceau de 2, est employée pour optimiser le processus d'évaluation. Les expériences ont été menées sur un GPU A100.

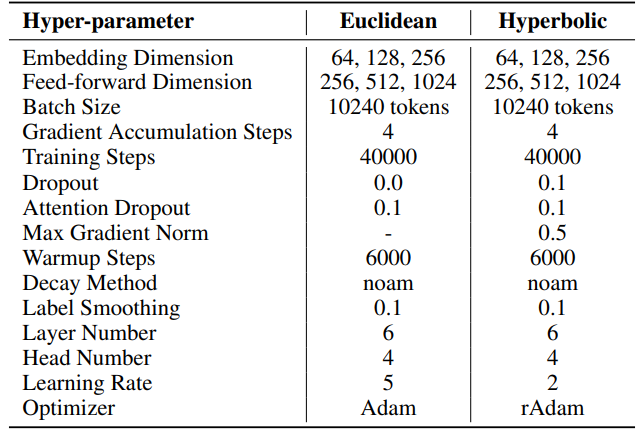
\ Pour SST, le nombre d'étapes par itération (T3) est fixé à 200. Chaque itération commence par une phase de préchauffage durant 20 étapes. Le nombre d'itérations par tour (T2) est déterminé par la formule T2 = d/r, où d représente la dimension d'intégration et r désigne le rang utilisé dans SST.

\ \ Tableau 6: Hyperparamètres sur IWSLT'14 pour Transformer euclidien et hyperbolique.

\ \ \

\ \ Pour SST, le nombre d'étapes par itération (T3) est fixé à 200 pour Multi30K et 400 pour IWSLT'17. Chaque itération commence par une phase de préchauffage durant 20 étapes. Le nombre d'itérations par tour (T2) est déterminé par la formule T2 = d/r, où d représente la dimension d'intégration et r désigne le rang utilisé dans SST

F.3 Hyperparamètres de la Génération de Langage Naturel

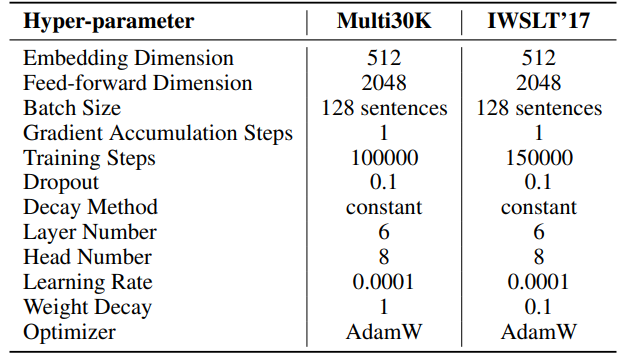
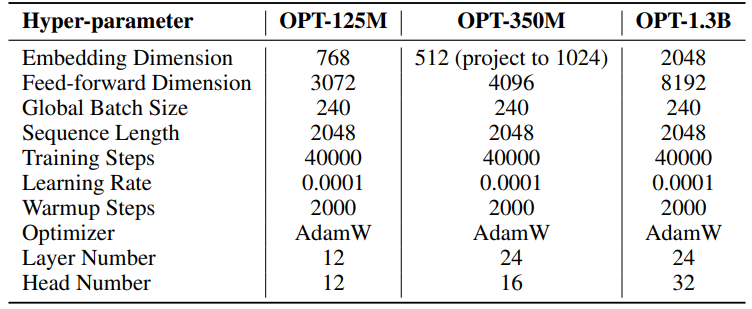
Les hyperparamètres de nos expériences sont détaillés dans le Tableau 8. Nous employons un préchauffage linéaire de 2000 étapes suivi d'un taux d'apprentissage stable, sans décroissance. Un taux d'apprentissage plus élevé (0,001) est utilisé uniquement pour les paramètres de rang faible (U, VT et Σ pour SST, B et A pour LoRA et ReLoRA*. Le total des jetons d'entraînement pour chaque expérience est de 19,7 milliards, soit environ 2 époques d'OpenWebText. L'entraînement distribué est facilité par la bibliothèque Accelerate [55] sur quatre GPU A100 sur un serveur Linux.

\ \ Tableau 7: Hyperparamètres sur Multi30K et IWSLT'17 pour Transformer vanilla.

\ \ \ Tableau 8: Hyperparamètres pour les modèles OPT

F.4 Hyperparamètres des Réseaux de Neurones Graphiques Hyperboliques

Nous utilisons HyboNet [12] comme modèle de rang complet, avec les mêmes hyperparamètres que ceux utilisés dans HyboNet. Les expériences ont été menées sur un GPU A100.

\ Pour SST, le nombre d'étapes par itération (T3) est fixé à 100. Chaque itération commence par une phase de préchauffage durant 100 étapes. Le nombre d'itérations par tour (T2) est déterminé par la formule T2 = d/r, où d représente la dimension d'intégration et r désigne le rang utilisé dans SST.

\ Nous fixons le taux de dropout à 0,5 pour les méthodes LoRA et SST pendant la tâche de classification des nœuds sur le jeu de données Cora. C'est la seule déviation par rapport à la configuration HyboNet.

\ \ \

:::info Auteurs :

(1) Jialin Zhao, Centre d'Intelligence des Réseaux Complexes (CCNI), Laboratoire Tsinghua du Cerveau et de l'Intelligence (THBI) et Département d'Informatique ;

(2) Yingtao Zhang, Centre d'Intelligence des Réseaux Complexes (CCNI), Laboratoire Tsinghua du Cerveau et de l'Intelligence (THBI) et Département d'Informatique ;

(3) Xinghang Li, Département d'Informatique ;

(4) Huaping Liu, Département d'Informatique ;

(5) Carlo Vittorio Cannistraci, Centre d'Intelligence des Réseaux Complexes (CCNI), Laboratoire Tsinghua du Cerveau et de l'Intelligence (THBI), Département d'Informatique et Département de Génie Biomédical, Université Tsinghua, Pékin, Chine.

:::

:::info Cet article est disponible sur arxiv sous licence CC by 4.0 Deed (Attribution 4.0 International).

:::

Clause de non-responsabilité : les articles republiés sur ce site proviennent de plateformes publiques et sont fournis à titre informatif uniquement. Ils ne reflètent pas nécessairement les opinions de MEXC. Tous les droits restent la propriété des auteurs d'origine. Si vous estimez qu'un contenu porte atteinte aux droits d'un tiers, veuillez contacter service@support.mexc.com pour demander sa suppression. MEXC ne garantit ni l'exactitude, ni l'exhaustivité, ni l'actualité des contenus, et décline toute responsabilité quant aux actions entreprises sur la base des informations fournies. Ces contenus ne constituent pas des conseils financiers, juridiques ou professionnels, et ne doivent pas être interprétés comme une recommandation ou une approbation de la part de MEXC.

Partager des idées