使用圆弧段进行曲线近似的更简单公式

链接表

摘要

1 引言

2 曲线的平面化和弧近似

3 欧拉螺线及其平行曲线

4 平面化平行曲线

5 弧近似的误差度量

6 渐屈线

7 从三次贝塞尔曲线转换为欧拉螺线

8 GPU实现

9 结果

结论、未来工作和参考文献

\

弧近似的误差度量

用一系列弧段近似曲线的问题有大量文献，但已发表的解决方案都不太适合我们的应用。Meek和Walton[2004]使用"先切后测量"的自适应细分方案考虑了用弧近似欧拉螺线的具体问题，但他们的解决方案质量较差；它的复杂度为𝑂(1/𝑛²)，而实际上可以达到𝑂(1/𝑛³)。Narayan[2014]对结果进行了"轻微"改进。

\ 文献中也包含最优结果，即Maier[2014]和Nuntawisuttiwong与Dejdumrong[2021]的工作，但代价相当高；两种方法都声称时间复杂度为𝑂(𝑛²)。所有这些结果的共同点是它们在解决一个更难的问题：采用生成的弧序列必须是𝐺¹连续的约束。虽然这对许多应用是理想的，但对于渲染笔触轮廓来说并不需要。

\ 即使放宽这一约束，弧近似的角度不连续性与平面化为线段相比也很小。我们的方法基于一个简单的误差度量，风格类似于平面化为线段的度量。该度量的细节（特别是常数的调整）是通过经验获得的，尽管我们怀疑可以获得更严格的分析界限。在实践中，它确实效果很好；观察这一点的最佳方式是使用交互式测试工具，该工具在补充材料中提供。

提出的误差度量如下。长度为𝑠ˆ的曲线的估计距离误差为：

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

对于欧拉螺线段，𝜅′(𝑠)是常数，因此这个误差度量变得几乎微不足道。使用𝑛个细分，估计距离简单地为𝑠³𝜅′/120𝑛³。求解𝑛，我们得到𝑛 = 𝑠³√(|𝜅′|/120𝑑)个细分，这些细分按弧长均匀分布，因为细分密度在整个曲线上是恒定的，就像将弧平面化为线段的情况一样。值得注意的是，用弧段近似欧拉螺线平行曲线几乎与欧拉螺线到弧的近似一样简单。

\ 与平面化为线段一样，曲线的参数是原始欧拉螺线的弧长。细分密度然后是恒定的，只需对计算细分数量的公式进行小调整，考虑到由ℎ（半线宽）偏移产生的额外曲率变化。修订后的公式是：

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

这个公式是通过曲线拟合从欧拉螺线平行曲线到弧的近似测量误差值经验确定的，但也受到将一般误差度量公式应用于欧拉螺线平行曲线的解析方程并舍弃高阶项的启发。更严格的推导，理想情况下具有确定的误差界限，仍然是未来的工作。

\ 这个公式的一个结果是，由于误差是以ℎ的绝对值表示的，与符号无关，因此同一弧近似可用于笔触的两侧。参见图8，比较平面化为折线和用弧段近似的效果。在相同容差下，弧段版本的段数要少得多，同时保持非常高的视觉质量。

渐屈线

在原则上正确的描边规范[19]中，平行曲线仅对曲率

\

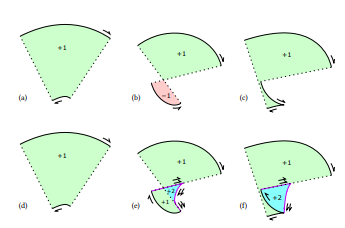
\ 不超过半宽度倒数的段足够。当超过时，必须绘制额外的段，包括原始曲线的渐屈线。一般来说，三次贝塞尔曲线的渐屈线是一个非常复杂的曲线，需要近似技术。相比之下，欧拉螺线(𝜅 = 𝑎𝑠)的渐屈线是另一个具有简单Cesàro方程的螺线，即𝜅 = −𝑎⁻¹𝑠⁻³，这是渐屈线的一般结果，即对数美学曲线的渐屈线是另一条对数美学曲线[26]。

\ 平面化这个渐屈线也很简单；细分密度与𝑠⁻⁰·⁵成正比，其中𝑠是底层欧拉螺线的弧长参数（并平移使𝑠 = 0是拐点）。因此，积分是2√𝑠，逆积分只是平方。因此，平面化欧拉螺线的渐屈线比平面化其平行曲线更简单。

\ 添加渐屈线以实现强正确性的效果如图9所示。额外的渐屈线段和连接线输出两次，以使绕数一致并产生水密轮廓。所有绕数都是正的，因此使用非零绕数规则渲染会产生正确的最终渲染。

:::info 作者：

1. Raph Levien
2. Arman Uguray

:::

:::info 本论文可在arxiv上获取，采用CC 4.0许可证。

:::

\