消融研究证实动态费率对RECKONING性能的必要性

链接表

摘要和1. 引言

1. 背景

2. 方法

3. 实验

   4.1 多跳推理性能

   4.2 带干扰项的推理

   4.3 对真实世界知识的泛化

   4.4 运行时间分析

   4.5 记忆知识

4. 相关工作

5. 结论、致谢和参考文献

\ A. 数据集

B. 带干扰项的上下文推理

C. 实现细节

D. 自适应学习率

E. 大型语言模型实验

D 自适应学习率

先前的工作[3, 4]表明，在步骤和参数之间共享的固定学习率不利于系统的泛化性能。相反，[3]建议为

\

\

\ 每个网络层和内循环中的每个适应步骤学习一个学习率。层参数可以学习在每个步骤动态调整学习率。为了在内循环中自适应地控制学习率α，我们将α定义为一组可调整变量：α = {α0, α1, …αL}，其中L是层数，对于每个l = 0, …, L，αl是一个具有N个元素的向量，给定预定义的内循环步数N。内循环更新方程则变为

\

\

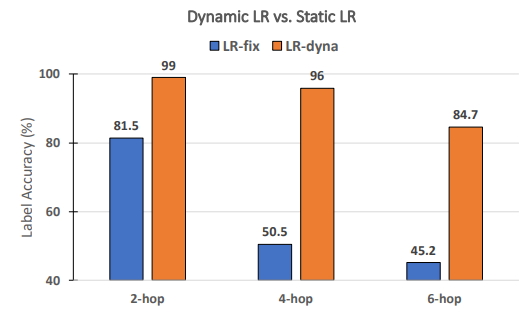
\ 动态学习率对RECKONING的性能是否必要？ 遵循元学习的先前工作[3, 4]，我们为RECKONING动态学习一组每步每层的学习率。在这项消融研究中，我们分析内循环的动态学习率是否能有效提高外循环推理性能。同样，我们固定其他实验设置并将内循环步数设为4。如图8所示，当使用静态学习率（即所有层和内循环步骤共享一个恒定学习率）时，性能大幅下降（平均下降34.2%）。对于需要更多推理跳数的问题，性能下降更为显著（4跳下降45.5%，6跳下降39.5%），这证明了在我们框架的内循环中使用动态学习率的重要性。

\

\

:::info 作者：

(1) Zeming Chen，EPFL (zeming.chen@epfl.ch)；

(2) Gail Weiss，EPFL (antoine.bosselut@epfl.ch)；

(3) Eric Mitchell，斯坦福大学 (eric.mitchell@cs.stanford.edu)'；

(4) Asli Celikyilmaz，Meta AI研究院 (aslic@meta.com)；

(5) Antoine Bosselut，EPFL (antoine.bosselut@epfl.ch)。

:::

:::info 本论文可在arxiv上获取，遵循CC BY 4.0 DEED许可。

:::

\