贪婪算法如何塑造区块链网络中的矿工奖励

链接表

摘要和1. 引言

1.1 我们的方法

1.2 我们的结果与路线图

1.3 相关工作

1. 模型和热身及2.1 区块链模型

   2.2 矿工

   2.3 博弈模型

   2.4 热身：贪婪分配函数

2. 确定性情况和3.1 确定性上界

   3.2 即时偏好类分配函数

3. 随机情况

4. 讨论和参考文献

• A. 第2、3节的缺失证明
• B. 第4节的缺失证明
• C. 词汇表

\

2.3 博弈模型

我们研究对手与矿工之间的博弈。这一视角旨在量化矿工在将当前已知交易分配到即将到来的区块时，由于对未来交易的不完整知识而可能损失的收益。在这方面，系统中活跃的用户可以被视为一个全知的对抗性"自然"，它创建最坏情况的交易计划。分配函数对对手将发送的未来交易没有任何了解，因此基于先前交易所揭示的部分信息进行的最优规划可能不是最佳行动方案。然而，令人惊讶的是，我们稍后会证明事实确实如此。给定矿工的折扣率，在包含最高手续费的交易和最低TTL的交易之间存在概念上的张力。因此，分配函数x的质量是通过将其与面对最坏情况对手ψ时的最佳可能函数x'进行比较来量化的。由此产生的量称为x的竞争比率。为了与数据包调度文献保持兼容，我们将竞争比率定义为最佳离线性能除以分配函数的在线性能，而不是相反，因此我们有Rx ≥ 1。通过找到保证良好性能的分配函数可以获得上界，而通过证明没有分配函数能保证更好的性能可以获得下界。

\ \

\ \ \

2.4 热身：贪婪分配函数

贪婪分配函数，在定义2.6中定义，也许是数据包调度问题的经典算法，并在之前的文献中针对未折扣情况进行了探索。此外，经验证据表明，大多数矿工贪婪地将交易分配到区块中。先前的研究表明，在比特币和以太坊中，支付更高手续费的交易通常在内存池中的等待时间更短，这意味着它们相对较快地被包含在区块中[MACG20; PORH22; TFWM21; LLNZZZ22]。实际上，比特币核心（比特币客户端的参考实现）和geth（以太坊最流行的执行客户端）的默认交易选择算法都基于手续费对交易进行优先排序，尽管两者的默认行为都可以被覆盖。因此，了解这种方法的性能很有意义。

\ 定义2.6（贪婪分配函数）。给定某个交易集合S，贪婪分配函数选择集合S中存在的支付最高的交易，忽略TTL：

\

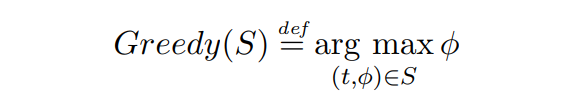
\ 如果有多个交易具有相同的手续费，则优先选择TTL最低的交易。

\ 在例2.7中，我们说明贪婪的性能如何依赖于折扣率。

\ 例2.7。 我们检查贪婪在给定以下对手ψ的情况下的性能。

\

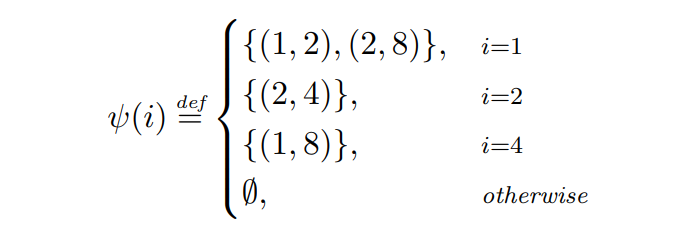
\ 由ψ定义的交易计划如图1所示。在第1轮，对手广播两笔交易：(1, 2)在轮末到期，手续费为2，以及(2, 4)支付等于4的手续费并在下一轮末到期。由于贪婪优先考虑手续费更高的交易，它将分配(2, 4)，而让另一笔交易过期。在下一轮，对手广播一笔TTL为2且手续费为6的单一交易，这是贪婪在该轮唯一可用的交易，因此将被分配。在第3步，对手不发出任何交易，而在第4步，一笔交易(1, 8)被广播，然后被贪婪分配。

\

\

\ 在引理2.8中，我们限定贪婪的竞争比率，作为折扣率的函数。

\

\

\

\

:::info 作者：

(1) Yotam Gafni，魏茨曼研究所 (yotam.gafni@gmail.com)；

(2) Aviv Yaish，耶路撒冷希伯来大学 (aviv.yaish@mail.huji.ac.il)。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0 DEED许可证。

:::

\