虫洞如何加速十亿边图中的路径查找

链接表

摘要和1. 引言

1.1 我们的贡献

1.2 设置

1.3 算法

1. 相关工作

2. 算法

   3.1 结构分解阶段

   3.2 路由阶段

   3.3 WormHole的变体

3. 理论分析

   4.1 预备知识

   4.2 内环的次线性

   4.3 近似误差

   4.4 查询复杂度

4. 实验结果

   5.1 WormHole𝐸, WormHole𝐻和BiBFS

   5.2 与基于索引方法的比较

   5.3 WormHole作为基元：WormHole𝑀

参考文献

1.1 我们的贡献

我们设计了一种新算法WormHole，它创建了一个数据结构，通过利用许多社交和信息网络的典型结构来回答多个最短路径查询。WormHole简单、易于实现，并有理论支持。我们提供了它的几个变体，每个变体适用于不同的设置，在各种网络数据集上展示了出色的实证结果。以下是其一些关键特点：

\ • 性能-准确度权衡。 据我们所知，我们的算法是大型网络中第一个近似次线性最短路径算法。我们允许小的加性误差，这导致了预处理时间/空间和每次查询时间之间的权衡，并使我们能够提出

\

\ 一个具有高效预处理和快速查询时间的解决方案。值得注意的是，我们最准确（但最慢）的变体WormHole𝐸具有近乎完美的准确度：超过90%的查询没有加性误差，在所有网络中，超过99%的查询的加性误差最多为2。详情请参见表3。

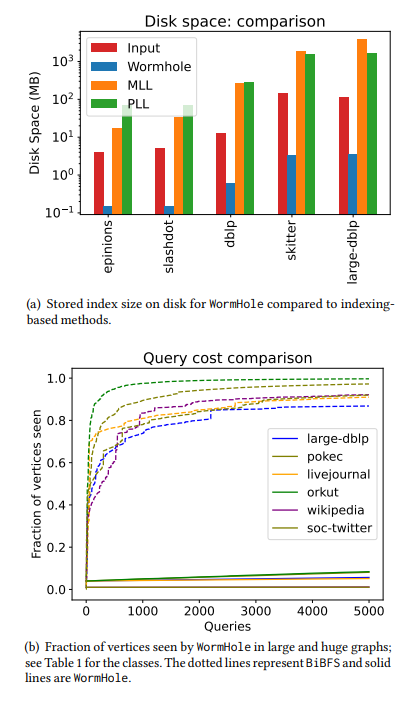
\ • 极快的设置时间。 即使对于拥有十亿边的图，我们最长的索引构建时间也只有两分钟。作为参考，PLL和MLL在我们测试的一半网络上超时，而对于PLL和MLL确实完成运行的中等规模图，WormHole索引构建速度快100倍。也就是说，WormHole在几秒钟内完成，而PLL需要几小时。参见表4和表5。这种快速设置时间是通过使用次线性大小的索引实现的。对于我们考虑的最大网络，只需要取约1%的节点作为索引就能获得较小的平均加性误差 - 参见表1。对于较小的网络，可能高达6%。

\ • 快速查询时间。 与BiBFS相比，普通版本WormHole𝐸（没有任何基于索引的优化）对几乎所有图都快2倍，对我们测试的三个最大图快4倍以上。简单变体WormHole𝐻以牺牲一些准确度为代价实现了数量级的改进：在几乎所有图上一致快20倍，对于我们拥有的最大图快180倍以上。完整比较请参见表3。基于索引的方法通常在微秒级回答查询；上述两种变体仍在毫秒级范围内。

\ • 结合WormHole和最先进技术。WormHole通过存储一小部分顶点并在其上计算精确的最短路径来工作。对于任意查询，我们通过这个子集（我们称之为核心）路由我们的路径。我们利用这一见解提供第三个变体WormHole𝑀，通过在核心上实现最先进的最短路径算法MLL。这实现了与MLL相当的查询时间（具有与WormHole𝐻相同的准确度保证），但设置成本只是一小部分，并且可以在MLL无法终止的大规模图上运行。我们在§5.3中探讨了这种组合方法，并在表6中提供了统计数据。

\ • 次线性查询复杂度。 查询复杂度指的是算法查询的顶点数量。在有限查询访问模型中，查询节点会显示其邻居列表（参见§1.2），我们算法的查询复杂度随着距离/最短路径查询数量的增加而表现良好。为了回答5000个近似最短路径查询，我们的算法对大多数网络只观察了1%到20%的节点。相比之下，BiBFS需要查看超过90%的图才能回答几百个最短路径查询。比较请参见图2和图5。

\ • 关于误差和性能的可证明保证。 在§4中，我们证明了一系列理论结果，补充和解释了实证性能。以下非正式陈述的结果是针对具有幂律度分布的Chung-Lu随机图模型[15-17]证明的。

\ 定理1.1（非正式）。在具有幂律指数𝛽∈(2,3)的n个顶点的Chung-Lu随机图𝐺中，WormHole以高概率具有以下保证：

\

\

:::info 作者：

(1) Talya Eden，巴伊兰大学 (talyaa01@gmail.com)；

(2) Omri Ben-Eliezer，麻省理工学院 (omrib@mit.edu)；

(3) C. Seshadhri，加州大学圣克鲁兹分校 (sesh@ucsc.edu)。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0许可证。

:::

\