这里没有赢家：为什么每个"公平"的加密货币拍卖最终都变得微不足道

链接表

摘要和1. 引言

1.1 技术概述

1.2 相关工作

1. 模型和预备知识及2.1 交易费用机制

   2.2 TFM的理想特性

2. 理解OCA

   3.1 SCP和OCA之间的区别

   3.2 OCA防护TFM的有用预备结果

3. 确定性OCA防护机制

4. 随机化OCA防护机制

5. 讨论和参考文献

   \

A. 缺失的证明

B. 非匿名确定性机制

4 确定性OCA防护机制

例3.6表明，一般来说，DSIC和1-OCA防护性质不足以保证零收益。我们现在证明，对于确定性机制，添加MMIC属性足以获得一般的0收益结果。

\ 定理4.1. 每个确定性DSIC+MMIC+1-OCA防护机制都有0矿工收益。

\

\ 然而，即使移除DSIC条件，我们也能提供有意义的特征描述。在引理4.3中给出的特征描述仍然非常相似，尽管在决定支付规则方面有更多自由。

\

\ 我们得出结论，所有分配值的销毁量是某个常数R。现在我们比较R与分配规则中的r。

\ 我们得出R = r的结论，这产生了指定的特征描述。

\ 这使我们能够更一般地进一步描述确定性1-OCA防护机制的分配和销毁规则。

\ 引理4.4. 任何1-OCA防护确定性机制a, p, β都恰好具有以下形式：对于某个r ≥ 0，该机制将物品分配给出价最高且高于r的竞标者，或者根本不分配物品。每当分配时，销毁量恰好为r。即，

\

\

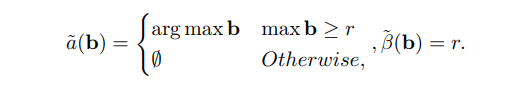
\ 我们现在可以精确地描述两类机制：DSIC+1-OCA防护确定性机制类别和MMIC+1-OCA防护确定性机制类别。

\

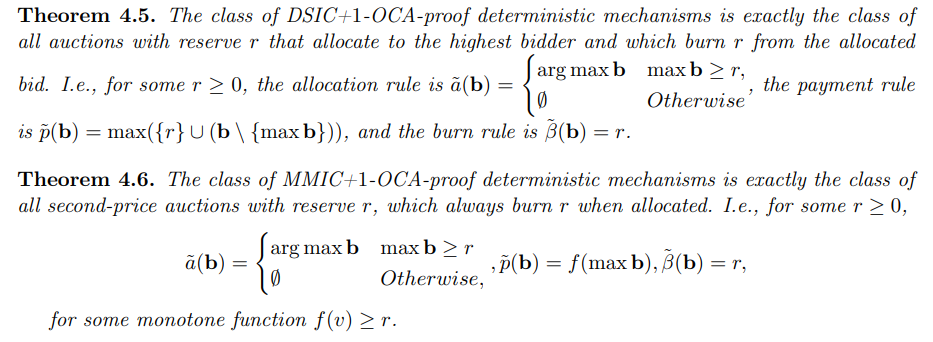
\ 这些精确的特征描述现在使我们能够得出以下结论：

定理4.7. 永不分配物品是唯一的DSIC+MMIC+1-OCA防护确定性机制。

\ 证明。这源于定理4.5和定理4.6，因为这些结果中描述的两类机制只有平凡机制是共同的（取r = ∞）。为了直观地理解这一点，考虑定理4.5中的具有保留价r和常数销毁r的第二价格拍卖类别。第二价格拍卖不是MMIC，因为矿工可以添加一个接近获胜出价的虚假竞标者来增加支付。

\

5 随机化OCA防护机制

我们现在将讨论扩展到随机化OCA防护机制。对于随机化机制，我们考虑更强的OCA防护概念（而不是1-OCA防护）。我们这样做是为了避免定义中的混乱，因为在随机化机制中，获胜联盟很可能必须包括所有竞标者（因为每个人都有一定的获胜概率）。

\ 我们现在考虑机制的一个自然属性：

\ 推论5.4. 根据引理5.3，DSIC+OCA防护尺度不变机制不销毁费用（即，其销毁规则是常数零函数），而从引理3.5我们得知，DSIC+MMIC+OCA防护机制在单一竞标者情况下的支付等于销毁量。因此，在单一竞标者情况下，我们必须有0支付，所以在单一竞标者情况下，物品要么总是被分配，要么从不被分配。

\ 引理5.5. 对于DSIC+MMIC+OCA防护机制，如果在单一竞标者情况下物品总是或从不被分配，则该机制必须是平凡的。

\

\ 因此，作为推论5.4和引理5.5的直接结果，我们有：

推论5.6. 不存在非平凡的尺度不变DSIC+MMIC+OCA防护机制。

\ 我们在引理5.5中使用的论证可以扩展，使我们也能排除满足我们称为常数总分配概率（CTPA）属性的拍卖类别，该属性在定义5.7中定义。这是一个有趣的拍卖类别，因为它包括所有高效拍卖（属于常数总概率1的分配类别），包括第一价格和第二价格拍卖。

\

\

\

\ 因此，根据可行性方程(1)：

\ 注意，这是引理5.12的左侧，我们考虑出价B · b, A · b。我们因此可以重复我们如何推导方程(14)（对于出价A · b, A · b的情况），并通过考虑矿工省略出价B · b，得到：

\ 此外，对于两个竞标者的情况，我们可以显示函数应该"偏好"更高竞标者的有用上下界：

\

\

\

\

:::info 作者：

(1) Yotam Gafni，魏茨曼研究所 (yotam.gafni@gmail.com)；

(2) Aviv Yaish，耶路撒冷希伯来大学 (aviv.yaish@mail.huji.ac.il)。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0 DEED许可证。

:::

\