了解虫洞路由中的近似误差和查询复杂性

链接表

摘要和1. 引言

1.1 我们的贡献

1.2 设定

1.3 算法

1. 相关工作

2. 算法

   3.1 结构分解阶段

   3.2 路由阶段

   3.3 WormHole的变体

3. 理论分析

   4.1 预备知识

   4.2 内环的次线性

   4.3 近似误差

   4.4 查询复杂度

4. 实验结果

   5.1 WormHole𝐸, WormHole𝐻和BiBFS

   5.2 与基于索引方法的比较

   5.3 WormHole作为基元：WormHole𝑀

参考文献

4.3 近似误差

现在我们有了一个包含Chung-Lu核心的次线性内环，我们必须证明通过它路由路径只会产生很小的惩罚。直观上，内环越大，满足这一点就越容易：如果内环是整个图，这个陈述就变得显而易见。因此，挑战在于证明即使使用次线性内环，我们也能在准确性方面获得强有力的保证。我们证明WormHole对所有点对产生的加性误差最多为𝑂(loglog𝑛)，这比直径Θ(log𝑛)小得多。

\

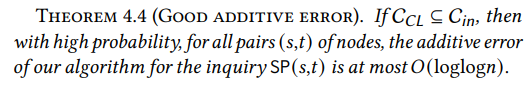
\ 上述结果即使在最坏情况下也以高概率成立。即，对于图中所有顶点对(𝑠,𝑡)，WormHole返回的路径长度最多比𝑠和𝑡之间的实际距离高𝑂(loglog𝑛)。这显然意味着WormHole的平均加性误差，以高概率，被相同的量所限制。

\

\

4.4 查询复杂度

回顾本文中的节点查询模型（见§1.2）：从单个节点开始，我们被允许迭代地进行查询，每次查询检索我们选择的节点𝑣的邻居列表。我们关注的是查询复杂度，即进行特定操作所需的查询次数。

\ \

\ \ 第一个结果是我们性能的上界。

\ \

\ \ 证明概要。对于给定的查询SP(𝑢, 𝑣)，我们给出从𝑢开始的BFS的查询复杂度上界，对𝑣也类似；总查询复杂度是这两个量的总和。

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info 作者：

(1) Talya Eden，巴伊兰大学 (talyaa01@gmail.com)；

(2) Omri Ben-Eliezer，麻省理工学院 (omrib@mit.edu)；

(3) C. Seshadhri，加州大学圣克鲁兹分校 (sesh@ucsc.edu)。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0许可证。

:::

\