使用圓弧段進行曲線近似的更簡單公式

目錄連結

摘要

1 引言

2 曲線的平面化與弧形近似

3 歐拉螺線及其平行曲線

4 平面化平行曲線

5 弧形近似的誤差度量

6 演化曲線

7 從三次貝茲曲線轉換為歐拉螺線

8 GPU 實現

9 結果

結論、未來工作與參考文獻

\

弧形近似的誤差度量

用一系列弧段近似曲線的問題有大量文獻，但已發表的解決方案都不太適合我們的應用。Meek 和 Walton [2004] 使用「先切割後測量」的自適應細分方案考慮了用弧形近似歐拉螺線的特定問題，但他們的解決方案質量較差；它的複雜度為 𝑂(1/𝑛 2 )，而實際上可以達到 𝑂(1/𝑛 3 )。Narayan [2014] 對結果進行了「輕微」改進。

\ 文獻中也包含最佳結果，即 Maier [2014] 和 Nuntawisuttiwong 與 Dejdumrong [2021]，但代價相當高；兩種方法都聲稱時間複雜度為 𝑂(𝑛 2 )。所有這些結果的共同點是它們正在解決一個更難的問題：採用生成的弧序列必須是 𝐺 1 連續的約束。雖然這對許多應用來說是理想的，但對於渲染筆劃輪廓來說並不需要。

\ 即使放寬這個約束，弧形近似的角度不連續性與平面化為直線相比也很小。我們的方法基於一個簡單的誤差度量，風格類似於平面化為線段的度量。該度量的細節（特別是常數的調整）是通過實驗獲得的，儘管我們懷疑可以獲得更嚴格的分析界限。在實踐中，它確實效果很好；觀察這一點的最佳方式是使用互動測試工具，該工具在補充材料中提供。

提出的誤差度量如下。長度為 𝑠ˆ 的曲線的估計距離誤差為：

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

對於歐拉螺線段，𝜅 ′ (𝑠) 是常數，因此這個誤差度量變得幾乎微不足道。使用 𝑛 個細分，估計距離簡單地為 𝑠 3𝜅 ′ 120𝑛 3 。求解 𝑛，我們得到 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 個細分，這些細分按弧長均勻分布，因為細分密度在整個曲線上是恆定的，就像將弧平面化為線的情況一樣。值得注意的是，用弧段近似歐拉螺線平行曲線幾乎與將歐拉螺線近似為弧一樣簡單。

\ 與平面化為線一樣，曲線的參數是原始歐拉螺線的弧長。細分密度然後是恆定的，只需對計算細分數量的公式進行小調整，考慮到由 ℎ（半線寬）偏移產生的額外曲率變化。修訂後的公式是：

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

這個公式是通過曲線擬合從歐拉螺線平行曲線到弧的近似測量誤差值經驗確定的，但也受到將一般誤差度量公式應用於歐拉螺線平行曲線的分析方程並捨棄高階項的啟發。更嚴格的推導，理想情況下具有確定的誤差界限，仍然是未來的工作。

\ 這個公式的一個結果是，由於誤差是以 ℎ 的絕對值表示的，與符號無關，因此相同的弧近似可用於筆劃的兩側。請參見圖 8，比較平面化為折線和用弧段近似。在相同容差下，弧段版本的段數少得多，同時保持非常高的視覺質量。

演化曲線

在原則性、正確的筆劃規範 [19] 中，平行曲線僅對曲率

\

\ 不超過半寬度倒數的段足夠。當超過時，必須繪製額外的段，包括原始曲線的演化曲線。一般來說，三次貝茲曲線的演化曲線是一個非常複雜的曲線，需要近似技術。相比之下，歐拉螺線（𝜅 = 𝑎𝑠）的演化曲線是另一個具有簡單 Cesàro 方程的螺線，即 𝜅 = −𝑎 −1 𝑠 −3，這是演化曲線的一般結果，即對數美學曲線的演化曲線是另一條對數美學曲線 [26]。

\ 平面化這個演化曲線也很直接；細分密度與 𝑠 −0.5 成正比，其中 𝑠 是底層歐拉螺線的弧長參數（並平移使 𝑠 = 0 為拐點）。因此，積分為 2 √ 𝑠，而逆積分只是平方。因此，平面化歐拉螺線的演化曲線比平面化其平行曲線更簡單。

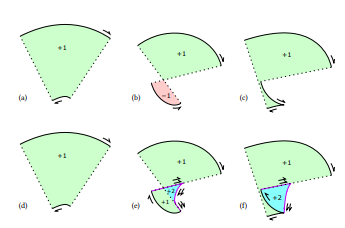
\ 添加演化曲線以實現強正確性的效果如圖 9 所示。額外的演化曲線段和連接線輸出兩次，以使繞數一致並產生水密輪廓。所有繞數都是正數，因此使用非零繞數規則渲染會產生正確的最終渲染。

:::info 作者：

1. Raph Levien
2. Arman Uguray

:::

:::info 本論文可在 Arxiv 上獲取，採用 CC 4.0 許可證。

:::

\