消融研究證實動態費率對 RECKONING 性能的必要性

連結表格

摘要和 1. 引言

1. 背景

2. 方法

3. 實驗

   4.1 多跳推理性能

   4.2 帶干擾項的推理

   4.3 對真實世界知識的泛化

   4.4 運行時間分析

   4.5 記憶知識

4. 相關工作

5. 結論、致謝和參考文獻

\ A. 數據集

B. 帶干擾項的上下文推理

C. 實現細節

D. 自適應學習率

E. 大型語言模型實驗

D 自適應學習率

先前的研究 [3, 4] 表明，在步驟和參數之間共享的固定學習率無法提高系統的泛化性能。相反，[3] 建議為

\

\

\ 每個網絡層和內循環中的每個適應步驟學習一個學習率。層參數可以學習在每個步驟動態調整學習率。為了在內循環中自適應地控制學習率 α，我們將 α 定義為一組可調整變量：α = {α0, α1, …αL}，其中 L 是層數，對於每個 l = 0, …, L，αl 是一個具有 N 個元素的向量，給定預定義的內循環步驟數 N。內循環更新方程則變為

\

\

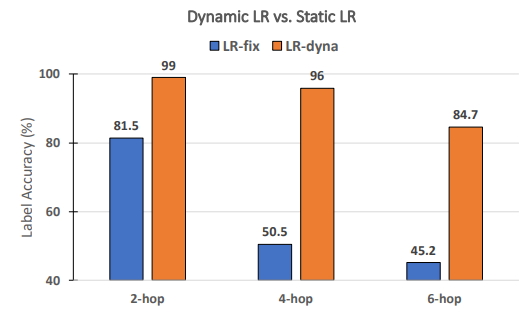
\ 動態學習率對 RECKONING 的性能是否必要？ 遵循元學習的先前工作 [3, 4]，我們為 RECKONING 動態學習一組每步每層的學習率。在這項消融研究中，我們分析內循環的動態學習率是否能有效提高外循環推理性能。同樣，我們固定其他實驗設置並將內循環步驟數設為 4。如圖 8 所示，當使用靜態學習率（即所有層和內循環步驟共享一個恆定學習率）時，性能大幅下降（平均下降了 34.2%）。對於需要更多推理跳躍的問題，性能下降更為顯著（4 跳下降了 45.5%，6 跳下降了 39.5%），這證明了在我們框架的內循環中使用動態學習率的重要性。

\

\

:::info 作者：

(1) Zeming Chen, EPFL (zeming.chen@epfl.ch);

(2) Gail Weiss, EPFL (antoine.bosselut@epfl.ch);

(3) Eric Mitchell, Stanford University (eric.mitchell@cs.stanford.edu)';

(4) Asli Celikyilmaz, Meta AI Research (aslic@meta.com);

(5) Antoine Bosselut, EPFL (antoine.bosselut@epfl.ch).

:::

:::info 本論文可在 Arxiv 上獲取，遵循 CC BY 4.0 DEED 許可證。

:::

\