這就是為什麼 AI 研究人員正在談論稀疏譜訓練
連結表
摘要和1. 引言
-
相關工作
-
低秩適應
3.1 LoRA和3.2 LoRA的限制
3.3 ReLoRA*
-
稀疏譜訓練
4.1 預備知識和4.2 使用Σ進行U、VT的梯度更新
4.3 為什麼SVD初始化很重要
4.4 SST平衡利用與探索
4.5 SST的記憶體高效實現和4.6 SST的稀疏性
-
實驗
5.1 機器翻譯
5.2 自然語言生成
5.3 雙曲圖神經網絡
-
結論與討論
-
更廣泛影響和參考文獻
補充資料
A. 稀疏譜訓練算法
B. 稀疏譜層梯度證明
C. 權重梯度分解證明
D. 增強梯度優於默認梯度的證明
E. SVD初始化零失真證明
F. 實驗細節
G. 奇異值剪枝
H. 評估SST和GaLore:記憶體效率的互補方法
I. 消融研究
A 稀疏譜訓練算法
B 稀疏譜層梯度證明
我們可以將W的微分表示為微分的總和:
\ \ 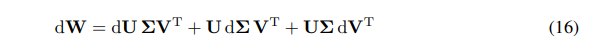
\ \ 我們有W梯度的鏈式法則:
\ \ 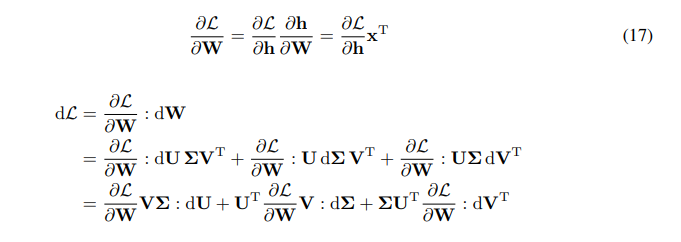
\ \ \ 
\
C 權重梯度分解證明
\ 
\
D 增強梯度優於默認梯度的證明
\ 
\ \ \ 
\ \ \ 
\ \ 由於只有更新方向重要,更新的規模可以通過改變學習率來調整。我們使用SST更新與全秩更新3倍之間差異的Frobenius範數來衡量相似性。
\ \ 
\
E SVD初始化零失真證明
\ 
F 實驗細節
F.1 SST的實現細節
\ 
\ \ \ 
\
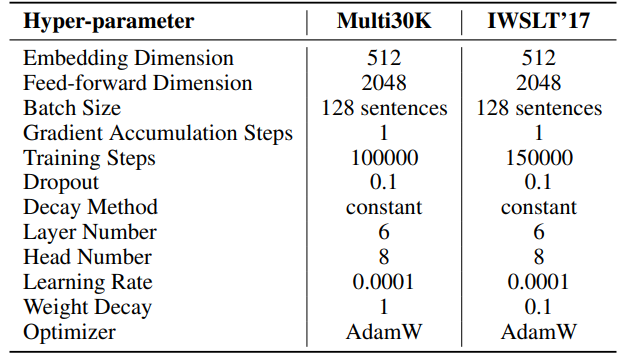
F.2 機器翻譯的超參數
IWSLT'14。 超參數可在表6中找到。我們採用與HyboNet [12]相同的代碼庫和超參數,該代碼庫源自OpenNMT-py [54]。最終模型檢查點用於評估。使用光束搜索,光束大小為2,以優化評估過程。實驗在一個A100 GPU上進行。
\ 對於SST,每次迭代的步數(T3)設為200。每次迭代以持續20步的預熱階段開始。每輪迭代次數(T2)由公式T2 = d/r確定,其中d表示嵌入維度,r表示SST中使用的秩。
\ \ 
\ \ \ 
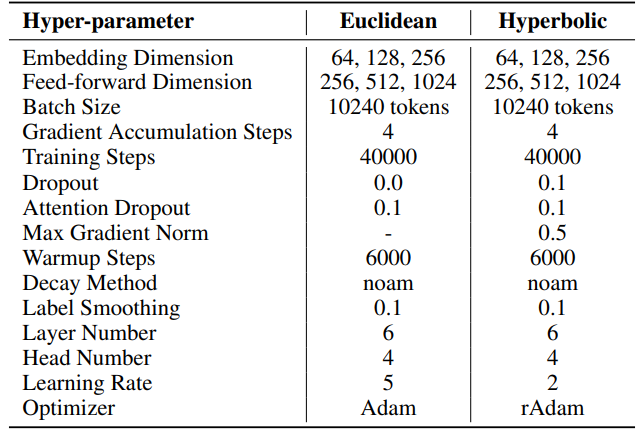
\ \ 對於SST,每次迭代的步數(T3)在Multi30K上設為200,在IWSLT'17上設為400。每次迭代以持續20步的預熱階段開始。每輪迭代次數(T2)由公式T2 = d/r確定,其中d表示嵌入維度,r表示SST中使用的秩
F.3 自然語言生成的超參數
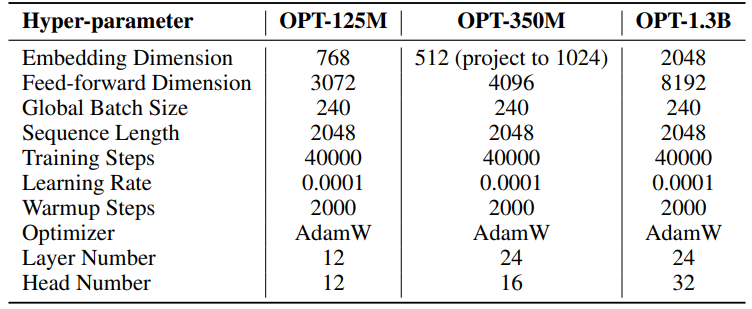
我們實驗的超參數詳見表8。我們採用2000步的線性預熱,然後是穩定的學習率,沒有衰減。較大的學習率(0.001)僅用於低秩參數(SST的U、VT和Σ,LoRA和ReLoRA*的B和A)。每個實驗的總訓練標記為19.7B,大約是OpenWebText的2個周期。分佈式訓練使用Accelerate [55]庫在Linux伺服器上的四個A100 GPU上進行。
\ 對於SST,每次迭代的步數(T3)設為200。每次迭代以持續20步的預熱階段開始。每輪迭代次數(T2)由公式T2 = d/r確定,其中d表示嵌入維度,r表示SST中使用的秩。
\ \ 
\ \ \ 
\
F.4 雙曲圖神經網絡的超參數
我們使用HyboNet [12]作為全秩模型,採用與HyboNet相同的超參數。實驗在一個A100 GPU上進行。
\ 對於SST,每次迭代的步數(T3)設為100。每次迭代以持續100步的預熱階段開始。每輪迭代次數(T2)由公式T2 = d/r確定,其中d表示嵌入維度,r表示SST中使用的秩。
\ 在Cora數據集的節點分類任務中,我們為LoRA和SST方法設置了0.5的丟棄率。這是唯一與HyboNet配置的偏差。
\ \ \
:::info 作者:
(1) 趙佳林,複雜網絡智能中心(CCNI),清華大學腦與智能實驗室(THBI)和計算機科學系;
(2) 張英濤,複雜網絡智能中心(CCNI),清華大學腦與智能實驗室(THBI)和計算機科學系;
(3) 李星航,計算機科學系;
(4) 劉華平,計算機科學系;
(5) Carlo Vittorio Cannistraci,複雜網絡智能中心(CCNI),清華大學腦與智能實驗室(THBI),計算機科學系和生物醫學工程系,中國北京。
:::
:::info 本論文可在arxiv上獲取,採用CC by 4.0 Deed (Attribution 4.0 International)許可證。
:::
\
您可能也會喜歡

持有最多投資者的 15 種 Altcoins 清單已發布

英國加密貨幣 ETN 市場在零售訪問恢復後競爭激烈 — 發行商將費用降低到 0.05%
