貪婪演算法如何塑造區塊鏈網絡中的礦工獎勵
連結表
摘要和 1. 引言
1.1 我們的方法
1.2 我們的結果與路線圖
1.3 相關工作
-
模型和熱身及 2.1 區塊鏈模型
2.2 礦工
2.3 遊戲模型
2.4 熱身:貪婪分配函數
-
確定性情況及 3.1 確定性上界
3.2 即時偏好類分配函數
-
隨機情況
-
討論和參考文獻
- A. 第 2、3 節的缺失證明
- B. 第 4 節的缺失證明
- C. 詞彙表
\
2.3 遊戲模型
我們研究對手與礦工之間的遊戲。這個視角旨在量化礦工因為對未來交易知識不完整而在分配當前已知交易到即將到來的區塊時可能損失的收益。在這方面,系統中活躍的用戶可以被視為一個全知的對抗性「自然」,它創造最壞情況的交易排程。分配函數對對手將發送的未來交易沒有知識,因此基於先前交易揭示的部分信息進行最佳規劃可能不是最佳行動方案。然而,令人驚訝的是,我們稍後會證明事實確實如此。考慮到礦工的折扣率,在包含手續費最高的交易和 TTL 最低的交易之間存在概念上的張力。因此,分配函數 x 的質量是通過將其與面對最壞情況對手 ψ 時的最佳可能函數 x′ 進行比較來量化的。由此產生的量稱為 x 的競爭比率。為了與封包排程文獻保持兼容,我們將競爭比率定義為最佳離線性能除以分配函數的在線性能,而不是相反,因此我們有 Rx ≥ 1。上界是通過找到保證良好性能的分配函數來獲得的,而下界是通過證明沒有分配函數能保證更好的性能來獲得的。
\ \ 
\ \ \
2.4 熱身:貪婪分配函數
貪婪分配函數,在定義 2.6 中定義,也許是封包排程問題的經典算法,並在先前文獻中針對未折扣情況進行了探討。此外,經驗證據表明大多數礦工貪婪地將交易分配到區塊中。先前的研究表明,在 Bitcoin 和 Ethereum 中,支付較高手續費的交易通常在記憶池中等待時間較短,這意味著它們相對較快地被包含在區塊中 [MACG20; PORH22; TFWM21; LLNZZZ22]。事實上,Bitcoin Core(Bitcoin 客戶端的參考實現)和 geth(Ethereum 最流行的執行客戶端)的默認交易選擇算法都基於手續費優先處理交易,儘管兩者的默認行為都可以被覆蓋。因此,了解這種方法的性能很有意義。
\ 定義 2.6(貪婪分配函數)。給定某個交易集合 S,貪婪分配函數選擇集合 S 中存在的支付最高的交易,忽略 TTL:
\ 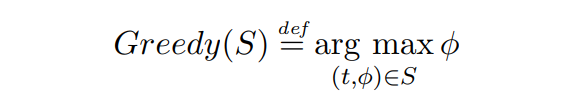
\ 如果有多個交易具有相同的手續費,則優先選擇 TTL 最低的交易。
\ 在例子 2.7 中,我們說明貪婪的性能如何依賴於折扣率。
\ 例子 2.7。 我們檢查貪婪在以下對手 ψ 下的性能。
\ 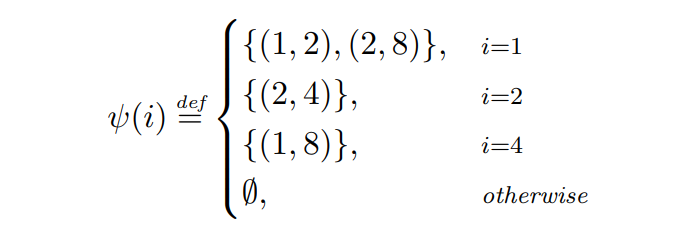
\ 由 ψ 定義的交易排程如圖 1 所示。在第 1 回合,對手廣播兩筆交易:(1, 2) 在回合結束時到期,手續費為 2,以及 (2, 4) 支付等於 4 的手續費並在下一回合結束時到期。因為貪婪優先處理手續費較高的交易,它將分配 (2, 4),而讓另一筆交易到期。在下一回合,對手廣播一筆 TTL 為 2 且手續費為 6 的單一交易,這是貪婪在該回合唯一可用的交易,因此將被分配。在第 3 步,對手不發出任何交易,而在第 4 步,一筆交易 (1, 8) 被廣播,然後被貪婪分配。
\ 
\ 
\ 在引理 2.8 中,我們限制貪婪的競爭比率,作為折扣率的函數。
\ 
\ 
\ 
\
:::info 作者:
(1) Yotam Gafni,魏茨曼研究所 (yotam.gafni@gmail.com);
(2) Aviv Yaish,耶路撒冷希伯來大學 (aviv.yaish@mail.huji.ac.il)。
:::
:::info 本論文可在 arxiv 上獲取,採用 CC BY 4.0 DEED 許可證。
:::
\
您可能也會喜歡

英國零售銷售放緩,因預算擔憂抑制消費

下一個100倍加密貨幣:Mutuum Finance (MUTM) 加入 Solana (SOL) 成為2025年頂級山寨幣投資選擇
