Toto 如何重新構想多頭注意力機制用於多變量預測

連結表格

1. 背景
2. 問題陳述
3. 模型架構
4. 訓練數據
5. 結果
6. 結論
7. 影響聲明
8. 未來方向
9. 貢獻
10. 致謝與參考文獻

附錄

3 模型架構

Toto 是一個僅解碼器的預測模型。這個模型採用了許多來自文獻的最新技術，並引入了一種新穎的方法來將多頭注意力機制應用於多變量時間序列數據（圖 1）。

\ 3.1 Transformer 設計

\ 用於時間序列預測的 Transformer 模型已經使用了各種編碼器-解碼器 [12, 13, 21]、僅編碼器 [14, 15, 17] 和僅解碼器架構 [19, 23]。對於 Toto，我們採用僅解碼器架構。解碼器架構已被證明具有良好的擴展性 [25, 26]，並允許任意預測範圍。因果性下一個區塊預測任務也簡化了預訓練過程。

\ 我們使用了一些最新的大型語言模型（LLM）架構中的技術，包括預標準化 [27]、RMSNorm [28] 和 SwiGLU 前饋層 [29]。

\ 3.2 輸入嵌入

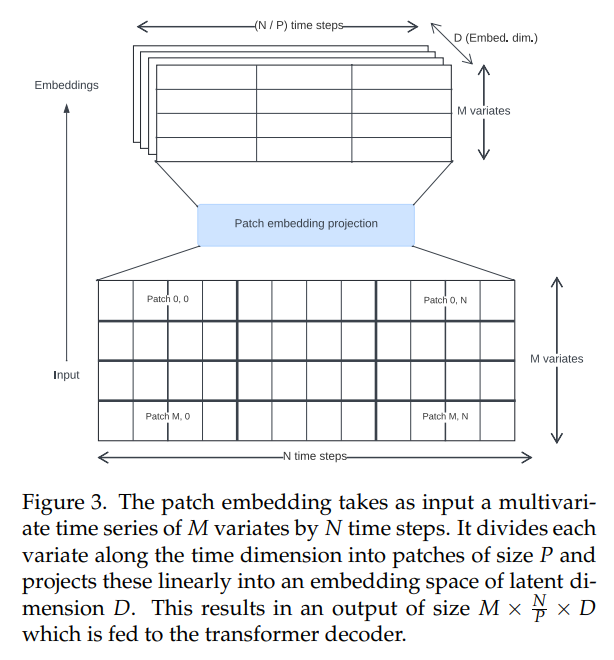
\ 文獻中的時間序列 Transformer 已經使用了各種方法來創建輸入嵌入。我們使用非重疊區塊投影（圖 3），這最初是為 Vision Transformers [30, 31] 引入的，並在時間序列上下文中由 PatchTST [14] 推廣。Toto 使用固定的區塊大小 32 進行訓練。

\

\ 3.3 注意力機制

\ 可觀測性指標通常是高基數、多變量時間序列。因此，理想的模型將原生處理多變量預測。它應該能夠分析時間維度（我們稱之為「時間方向」互動）和通道維度（我們稱之為「空間方向」互動，遵循 Datadog 平台中將指標的不同組或標籤集描述為「空間」維度的慣例）中的關係。

\ 為了同時建模空間和時間方向的互動，我們需要將傳統的多頭注意力架構 [11] 從一維調整為二維。文獻中已經提出了幾種方法來實現這一點，包括：

\ • 假設通道獨立，並僅在時間維度上計算注意力 [14]。這是高效的，但丟棄了所有關於空間方向互動的信息。

\ • 僅在空間維度上計算注意力，並在時間維度上使用前饋網絡 [17, 18]。

\ • 沿時間維度連接變量並計算每個空間/時間位置之間的完全交叉注意力 [15]。這可以捕捉每一個可能的空間和時間互動，但計算成本很高。

\ • 計算「因子化注意力」，其中每個 Transformer 區塊包含單獨的空間和時間注意力計算 [16, 32, 33]。這允許空間和時間混合，並且比完全交叉注意力更高效。然而，它使網絡的有效深度增加了一倍。

\ 為了設計我們的注意力機制，我們遵循這樣的直覺：對於許多時間序列，時間關係比空間關係更重要或更具預測性。作為證據，我們觀察到即使完全忽略空間方向關係的模型（如 PatchTST [14] 和 TimesFM [19]）仍然可以在多變量數據集上取得有競爭力的表現。然而，其他研究（例如 Moirai [15]）通過消融實驗表明，包含空間方向關係確實有一些明顯的好處。

\ 因此，我們提出了一種因子化注意力的新變體，我們稱之為「比例因子化空間-時間注意力」。我們使用交替的空間方向和時間方向注意力區塊的混合。作為可配置的超參數，我們可以改變時間方向與空間方向區塊的比例，從而允許我們為每種類型的注意力分配更多或更少的計算預算。對於我們的基本模型，我們選擇了每兩個時間方向注意力區塊配一個空間方向注意力區塊的配置。

\ 在時間方向注意力區塊中，我們使用因果遮罩和旋轉位置嵌入 [34] 與 XPOS [35]，以自回歸方式建模時間依賴特徵。相比之下，在空間方向區塊中，我們使用完全雙向注意力以保持協變量的排列不變性，並使用塊對角 ID 遮罩確保只有相關變量相互關注。這種遮罩允許我們將多個獨立的多變量時間序列打包到同一批次中，以提高訓練效率並減少填充量。

\ 3.4 概率預測頭

\ 為了在預測應用中有用，模型應該產生概率預測。時間序列模型中的常見做法是使用輸出層，其中模型回歸概率分佈的參數。這允許使用蒙特卡洛抽樣 [7] 計算預測區間。

\ 輸出層的常見選擇是正態分佈 [7] 和 Student-T 分佈 [23, 36]，它們可以提高對異常值的穩健性。Moirai [15] 通過提出一種新穎的混合模型，結合了高斯分佈、Student-T 分佈、對數正態分佈和負二項分佈輸出的加權組合，允許更靈活的殘差分佈。

\ 然而，現實世界的時間序列通常具有複雜的分佈，這些分佈具有異常值、重尾、極端偏斜和多模態性，難以擬合。為了適應這些情況，我們引入了更靈活的輸出似然。為此，我們採用了基於高斯混合模型（GMMs）的方法，它可以近似任何密度函數（[37]）。為了避免在存在異常值時的訓練不穩定性，我們使用 Student-T 混合模型（SMM），這是 GMMs 的穩健泛化 [38]，之前已經顯示出對建模重尾金融時間序列的前景 [39, 40]。該模型為每個時間步預測 k 個 Student-T 分佈（其中 k 是一個超參數），以及學習的權重。

\

\ 當我們執行推斷時，我們在每個時間戳從混合分佈中抽取樣本，然後將每個樣本重新輸入解碼器進行下一個預測。這使我們能夠在任何分位數產生預測區間，僅受樣本數量的限制；對於更精確的尾部，我們可以選擇在抽樣上花費更多的計算（圖 2）。

\ 3.5 輸入/輸出縮放

\ 與其他時間序列模型一樣，我們在將輸入數據通過區塊嵌入之前對其執行實例標準化，以使模型更好地泛化到不同尺度的輸入 [41]。我們將輸入縮放為零均值和單位標準差。然後將輸出預測重新縮放回原始單位。

\ 3.6 訓練目標

\ 作為僅解碼器模型，Toto 在下一個區塊預測任務上進行預訓練。我們最小化下一個預測區塊相對於模型分佈輸出的負對數似然。我們使用 AdamW 優化器 [42] 訓練模型。

\ 3.7 超參數

\ Toto 使用的超參數詳見表 A.1，總共有 1.03 億個參數。

\

:::info 作者：

(1) Ben Cohen (ben.cohen@datadoghq.com);

(2) Emaad Khwaja (emaad@datadoghq.com);

(3) Kan Wang (kan.wang@datadoghq.com);

(4) Charles Masson (charles.masson@datadoghq.com);

(5) Elise Rame (elise.rame@datadoghq.com);

(6) Youssef Doubli (youssef.doubli@datadoghq.com);

(7) Othmane Abou-Amal (othmane@datadoghq.com).

:::

:::info 本論文可在 Arxiv 上獲取，採用 CC BY 4.0 許可證。

:::

\