كيف تعيد توتو تصور الانتباه متعدد الرؤوس للتنبؤ متعدد المتغيرات
جدول الروابط
- الخلفية
- بيان المشكلة
- بنية النموذج
- بيانات التدريب
- النتائج
- الاستنتاجات
- بيان التأثير
- الاتجاهات المستقبلية
- المساهمات
- شكر وتقدير والمراجع
الملحق
3 بنية النموذج
توتو هو نموذج تنبؤ يعتمد على المفكك فقط. يستخدم هذا النموذج العديد من أحدث التقنيات من الأدبيات، ويقدم طريقة جديدة لتكييف الانتباه متعدد الرؤوس مع بيانات السلاسل الزمنية متعددة المتغيرات (الشكل 1).
\ 3.1 تصميم المحول
\ استخدمت نماذج المحول للتنبؤ بالسلاسل الزمنية بشكل متنوع هياكل المشفر-المفكك [12، 13، 21]، والمشفر فقط [14، 15، 17]، والمفكك فقط [19، 23]. بالنسبة لتوتو، نستخدم بنية المفكك فقط. لقد أظهرت هياكل المفكك قدرتها على التوسع بشكل جيد [25، 26]، وتسمح بآفاق تنبؤ عشوائية. تعمل مهمة التنبؤ بالرقعة التالية السببية أيضًا على تبسيط عملية التدريب المسبق.
\ نستخدم تقنيات من بعض أحدث هياكل نموذج اللغة الكبير (LLM)، بما في ذلك التطبيع المسبق [27]، وRMSNorm [28]، وطبقات SwiGLU الأمامية [29].
\ 3.2 تضمين المدخلات
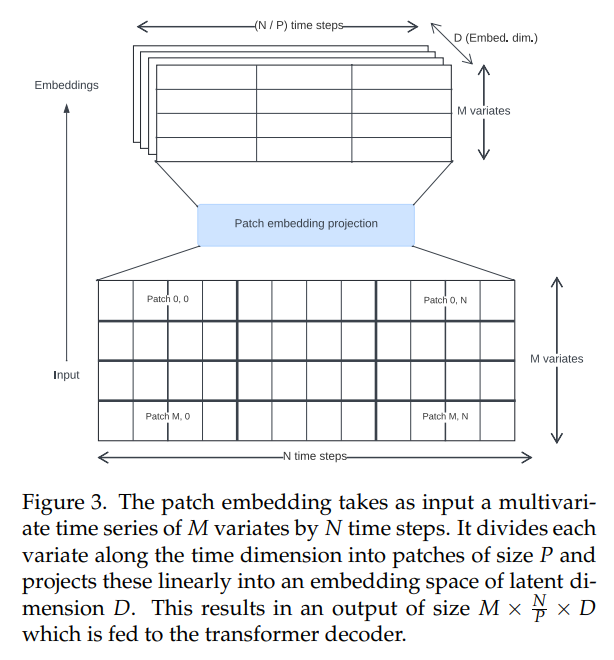
\ استخدمت محولات السلاسل الزمنية في الأدبيات مناهج مختلفة لإنشاء تضمينات المدخلات. نستخدم إسقاطات الرقع غير المتداخلة (الشكل 3)، التي تم تقديمها لأول مرة لمحولات الرؤية [30، 31] وأصبحت شائعة في سياق السلاسل الزمنية بواسطة PatchTST [14]. تم تدريب توتو باستخدام حجم رقعة ثابت قدره 32.
\ 
\ 3.3 آلية الانتباه
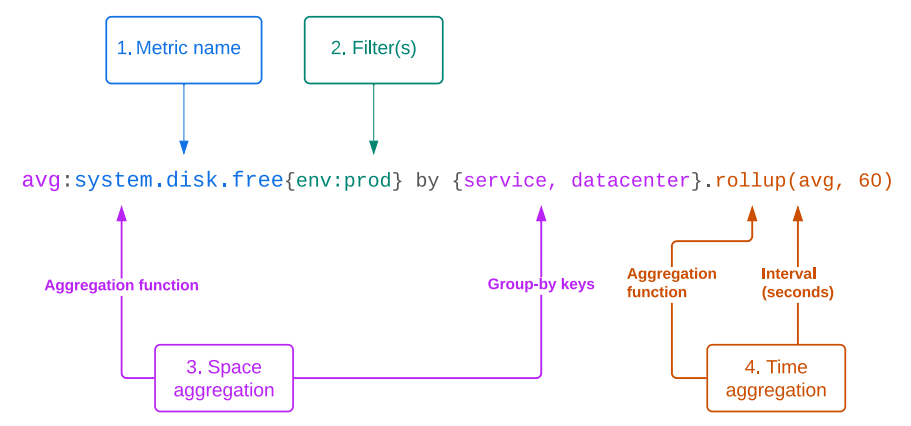
\ غالبًا ما تكون مقاييس المراقبة سلاسل زمنية متعددة المتغيرات وعالية الأهمية. لذلك، سيتعامل النموذج المثالي بشكل أصلي مع التنبؤ متعدد المتغيرات. يجب أن يكون قادرًا على تحليل العلاقات في بُعد الزمن (ما نشير إليه بالتفاعلات "الزمنية") وفي بُعد القناة (ما نشير إليه بالتفاعلات "المكانية"، اتباعًا للاتفاقية في منصة Datadog لوصف مجموعات مختلفة أو مجموعات العلامات لمقياس كبُعد "المكان").
\ من أجل نمذجة التفاعلات المكانية والزمنية، نحتاج إلى تكييف بنية الانتباه متعدد الرؤوس التقليدية [11] من بُعد واحد إلى بُعدين. تم اقتراح عدة مناهج في الأدبيات للقيام بذلك، بما في ذلك:
\ • افتراض استقلالية القناة، وحساب الانتباه فقط في بُعد الزمن [14]. هذا فعال، لكنه يتخلص من جميع المعلومات حول التفاعلات المكانية.
\ • حساب الانتباه فقط في البعد المكاني، واستخدام شبكة أمامية في البعد الزمني [17، 18].
\ • دمج المتغيرات على طول البعد الزمني وحساب الانتباه المتقاطع الكامل بين كل موقع مكاني/زمني [15]. يمكن أن يلتقط هذا كل تفاعل مكاني وزمني ممكن، لكنه مكلف من الناحية الحسابية.
\ • حساب "الانتباه المفكك"، حيث تحتوي كل كتلة محول على حساب انتباه مكاني وزمني منفصل [16، 32، 33]. هذا يسمح بالخلط المكاني والزمني، وهو أكثر كفاءة من الانتباه المتقاطع الكامل. ومع ذلك، فإنه يضاعف العمق الفعال للشبكة.
\ من أجل تصميم آلية الانتباه لدينا، نتبع الحدس بأنه بالنسبة للعديد من السلاسل الزمنية، تكون العلاقات الزمنية أكثر أهمية أو تنبؤًا من العلاقات المكانية. كدليل، نلاحظ أن حتى النماذج التي تتجاهل تمامًا العلاقات المكانية (مثل PatchTST [14] و TimesFM [19]) لا تزال قادرة على تحقيق أداء تنافسي على مجموعات البيانات متعددة المتغيرات. ومع ذلك، أظهرت دراسات أخرى (مثل Moirai [15]) من خلال الاستئصالات أن هناك بعض الفوائد الواضحة لتضمين العلاقات المكانية.
\ لذلك نقترح متغيرًا جديدًا من الانتباه المفكك، والذي نسميه "الانتباه المكاني-الزمني المفكك النسبي". نستخدم مزيجًا من كتل الانتباه المكانية والزمنية المتناوبة. كمعلمة فائقة قابلة للتكوين، يمكننا تغيير نسبة الكتل الزمنية إلى الكتل المكانية، مما يسمح لنا بتخصيص ميزانية حسابية أكثر أو أقل لكل نوع من الانتباه. بالنسبة لنموذجنا الأساسي، اخترنا تكوينًا مع كتلة انتباه مكانية واحدة لكل كتلتين زمنيتين.
\ في كتل الانتباه الزمنية، نستخدم التقنيع السببي والتضمينات الموضعية الدوارة [34] مع XPOS [35] من أجل نمذجة الميزات المعتمدة على الزمن بشكل تلقائي. في الكتل المكانية، على النقيض من ذلك، نستخدم الانتباه ثنائي الاتجاه الكامل من أجل الحفاظ على عدم تغير التبديل للمتغيرات المشتركة، مع قناع معرف قطري كتلي لضمان أن المتغيرات ذات الصلة فقط تنتبه لبعضها البعض. يسمح لنا هذا التقنيع بحزم سلاسل زمنية متعددة المتغيرات مستقلة متعددة في نفس الدفعة، من أجل تحسين كفاءة التدريب وتقليل كمية الحشو.
\ 3.4 رأس التنبؤ الاحتمالي
\ لكي يكون مفيدًا لتطبيقات التنبؤ، يجب أن ينتج النموذج تنبؤات احتمالية. الممارسة الشائعة في نماذج السلاسل الزمنية هي استخدام طبقة إخراج حيث يقوم النموذج بانحدار معلمات توزيع الاحتمالات. هذا يسمح بحساب فترات التنبؤ باستخدام أخذ عينات مونت كارلو [7].
\ الخيارات الشائعة لطبقة الإخراج هي Normal [7] و Student-T [23، 36]، والتي يمكن أن تحسن المتانة تجاه القيم المتطرفة. يسمح Moirai [15] بتوزيعات متبقية أكثر مرونة من خلال اقتراح نموذج مختلط جديد يتضمن مزيجًا موزونًا من مخرجات Gaussian و Student-T و Log-Normal و Negative-Binomial.
\ ومع ذلك، غالبًا ما يكون للسلاسل الزمنية في العالم الحقيقي توزيعات معقدة يصعب ملاءمتها، مع قيم متطرفة وذيول ثقيلة وانحراف شديد وتعدد الأنماط. من أجل استيعاب هذه السيناريوهات، نقدم احتمالية إخراج أكثر مرونة. للقيام بذلك، نستخدم طريقة تعتمد على نماذج خليط غاوسي (GMMs)، والتي يمكن أن تقرب أي دالة كثافة ([37]). لتجنب عدم استقرار التدريب في وجود القيم المتطرفة، نستخدم نموذج خليط Student-T (SMM)، وهو تعميم قوي لـ GMMs [38] أظهر سابقًا وعدًا لنمذجة السلاسل الزمنية المالية ذات الذيول الثقيلة [39، 40]. يتنبأ النموذج بـ k توزيعات Student-T (حيث k هي معلمة فائقة) لكل خطوة زمنية، بالإضافة إلى ترجيح متعلم.
\ 
\ عندما نقوم بالاستدلال، نأخذ عينات من توزيع الخليط في كل طابع زمني، ثم نغذي كل عينة مرة أخرى في المفكك للتنبؤ التالي. هذا يسمح لنا بإنتاج فترات تنبؤ عند أي كمية، محدودة فقط بعدد العينات؛ للحصول على ذيول أكثر دقة، يمكننا اختيار إنفاق المزيد من الحساب على أخذ العينات (الشكل 2).
\ 3.5 تحجيم المدخلات/المخرجات
\ كما هو الحال في نماذج السلاسل الزمنية الأخرى، نقوم بتطبيع المثيل على بيانات الإدخال قبل تمريرها عبر تضمين
قد يعجبك أيضاً

كادينا تلوم "ظروف السوق" مع خروج الفريق المؤسس، مما أدى إلى انهيار الرمز المميز

سوق التشفير يشتعل مع سولانا فوق 200 دولار، وBONK يرتفع بنسبة 13%، والبيع المسبق لـBlockDAG بقيمة 430 مليون دولار يحدث موجات
