لا فائزين هنا: لماذا تنتهي كل مزادات التشفير "العادلة" بشكل تافه

جدول الروابط

نبذة مختصرة و 1. مقدمة

1.1 نظرة عامة تقنية

1.2 الأعمال ذات الصلة

1. النموذج والمقدمات و 2.1 آليات رسوم التحويل

   2.2 المرغوب فيه TFM

2. فهم OCA

   3.1 الفرق بين SCP و OCA

   3.2 نتائج أولية مفيدة لآليات TFM المثبتة بـ OCA

3. آليات OCA-proof الحتمية

4. آليات OCA-proof العشوائية

5. المناقشة والمراجع

   \

أ. إثباتات مفقودة

ب. آليات حتمية غير مجهولة

4 آليات OCA-proof الحتمية

يوضح المثال 3.6 أنه بشكل عام، خصائص DSIC و 1-OCA-proofness ليست كافية لضمان إيرادات صفرية. نوضح الآن أنه بالنسبة للآليات الحتمية، فإن إضافة خاصية MMIC تكفي للحصول على نتيجة إيرادات عامة 0.

\ نظرية 4.1. كل آلية حتمية DSIC+MMIC+1-OCA-proof لها إيرادات تعدين 0.

\

\ ومع ذلك، يمكننا تقديم توصيف ذي معنى حتى عند إزالة شرط DSIC. يظل التوصيف، المقدم في اللمة 4.3، مشابهًا جدًا، وإن كان مع مزيد من الحرية لتحديد قاعدة الدفع.

\

\ نستنتج أن الحرق لجميع القيم المخصصة هو بعض الثابت R. نقارن الآن R مع r التي لدينا لقاعدة التخصيص.

\ نستنتج أن R = r، مما يؤدي إلى التوصيف المحدد.

\ هذا يسمح لنا بتوصيف قواعد التخصيص والحرق بشكل أكثر عمومية، لآليات 1-OCA-proof الحتمية.

\ لمة 4.4. أي آلية حتمية 1-OCA-proof a, p, β هي بالضبط على الشكل التالي: لبعض r ≥ 0، تخصص الآلية العنصر لأعلى مزايد بشرط أن تكون قيمته أعلى من r، أو لا تخصص العنصر على الإطلاق. عندما يتم التخصيص، يكون الحرق بالضبط r. أي،

\

\

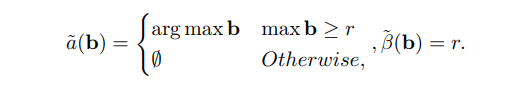
\ يمكننا الآن توصيف فئتين من الآليات بدقة: فئة آليات DSIC+1-OCA-proof الحتمية، وفئة آليات MMIC+1-OCA-proof الحتمية.

\

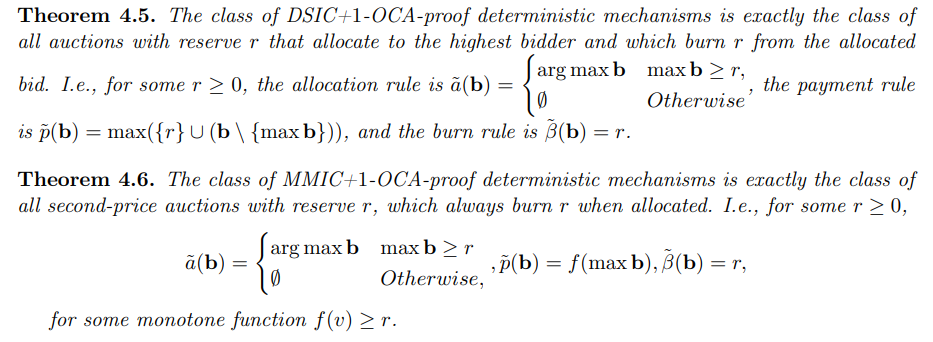
\ تسمح لنا هذه التوصيفات الدقيقة الآن بالختام بما يلي:

نظرية 4.7. عدم تخصيص العنصر أبدًا هو الآلية الحتمية الوحيدة DSIC+MMIC+1-OCA-proof.

\ إثبات. يتبع هذا من النظرية 4.5 والنظرية 4.6، حيث أن الفئتين الموصوفتين في هذه النتائج لديهما فقط الآلية البديهية المشتركة (أخذ r = ∞). لرؤية هذا بشكل حدسي، ضع في اعتبارك فئة مزادات السعر الثاني مع احتياطي r وحرق ثابت r من النظرية 4.5. مزادات السعر الثاني ليست MMIC لأن المنقب يمكنه إضافة مزايد وهمي قريب بشكل تعسفي من العرض الفائز لزيادة الدفع.

\

5 آليات OCA-proof العشوائية

نوسع الآن المناقشة إلى آليات OCA-proof العشوائية. بالنسبة للآليات العشوائية، نعتبر المفهوم الأقوى لـ OCA-proofness (بدلاً من 1-OCA-proofness). نفعل ذلك لتجنب الفوضى في التعريفات، لأنه في الآليات العشوائية قد يشمل التحالف الفائز بالضرورة جميع المزايدين (حيث أن لكل منهم احتمالية جزئية للفوز).

\ نعتبر الآن خاصية طبيعية للآليات:

\ نتيجة 5.4. بواسطة اللمة 5.3، آلية DSIC+OCA-proof ثابتة المقياس لا تحرق الرسوم (أي أن قاعدة الحرق الخاصة بها هي دالة الصفر الثابتة)، بينما من اللمة 3.5 نحصل على أن آلية DSIC+MMIC+OCAproof لها مدفوعات تساوي الحرق في حالة المزايد الواحد. لذلك، يجب أن يكون لدينا 0 مدفوعات في حالة المزايد الواحد، وبالتالي، في حالة المزايد الواحد، إما أن يتم تخصيص العنصر دائمًا أو لا يتم تخصيصه أبدًا.

\ لمة 5.5. بالنسبة لآلية DSIC+MMIC+OCA-proof، إذا تم تخصيص العنصر دائمًا أو لم يتم تخصيصه أبدًا في حالة المزايد الواحد، فيجب أن تكون الآلية بديهية.

\

\ وبالتالي، كنتيجة مباشرة للنتيجة 5.4 واللمة 5.5، لدينا:

نتيجة 5.6. لا توجد آلية DSIC+MMIC+OCA-proof ثابتة المقياس غير بديهية.

\ يمكن توسيع الحجة التي نستخدمها في اللمة 5.5 للسماح لنا أيضًا باستبعاد فئة المزادات التي تلبي خاصية نسميها احتمالية إجمالية ثابتة للتخصيص (CTPA)، والتي يتم تعريفها في التعريف 5.7. هذه فئة مثيرة للاهتمام من المزادات، لأنها تشمل جميع المزادات الفعالة (التي هي جزء من فئة الاحتمالية الإجمالية الثابتة 1 للتخصيص)، بما في ذلك مزادات السعر الأول والسعر الثاني.

\

\

\

\ وبالتالي بواسطة معادلة الجدوى (1):

\ لاحظ أن هذا هو الجانب الأيسر من اللمة 5.12 حيث نعتبر العروض B · b، A · b. يمكننا بالتالي تكرار الطريقة التي طورنا بها المعادلة (14) (لحالة العروض A · b، A · b) ومن خلال اعتبار أن المنقب يحذف العرض B · b، نحصل على:

\ علاوة على ذلك، في حالة وجود مزايدين، يمكننا إظهار حد أعلى وأدنى مفيد لمدى "تفضيل" الدالة للمزايد الأعلى:

\

\

\

\

:::info المؤلفون:

(1) يوتام غافني، معهد وايزمان (yotam.gafni@gmail.com);

(2) أفيف يعيش، الجامعة العبرية، القدس (aviv.yaish@mail.huji.ac.il).

:::

:::info هذه الورقة متاحة على arxiv تحت رخصة CC BY 4.0 DEED.

:::

\