Una fórmula más simple para la aproximación de curvas utilizando segmentos de arco

Tabla de enlaces

RESUMEN

1 INTRODUCCIÓN

2 APLANAMIENTO Y APROXIMACIÓN DE ARCO DE CURVAS

3 ESPIRALES DE EULER Y SUS CURVAS PARALELAS

4 CURVAS PARALELAS APLANADAS

5 MÉTRICAS DE ERROR PARA APROXIMACIÓN POR ARCOS

6 EVOLUTAS

7 CONVERSIÓN DE BÉZIERS CÚBICOS A ESPIRALES DE EULER

8 IMPLEMENTACIÓN EN GPU

9 RESULTADOS

CONCLUSIONES, TRABAJO FUTURO Y REFERENCIAS

\

MÉTRICAS DE ERROR PARA APROXIMACIÓN POR ARCOS

El problema de aproximar una curva mediante una secuencia de segmentos de arco tiene una extensa literatura, pero ninguna de las soluciones publicadas es adecuada para nuestra aplicación. El problema específico de aproximar una espiral de Euler mediante arcos es considerado en Meek y Walton [2004] utilizando un esquema de subdivisión adaptativa de "cortar y medir", pero su solución tiene baja calidad; escala como 𝑂(1/𝑛 2 ), mientras que 𝑂(1/𝑛 3 ) es alcanzable. El resultado fue mejorado "ligeramente" por Narayan [2014].

\ La literatura también contiene resultados óptimos, específicamente Maier [2014] y Nuntawisuttiwong y Dejdumrong [2021], pero a un costo considerable; ambos enfoques afirman tener una complejidad temporal de 𝑂(𝑛 2 ). La línea común para todos estos resultados es que están resolviendo un problema más difícil: adoptar la restricción de que la secuencia de arcos generada sea continua 𝐺 1. Aunque es deseable para muchas aplicaciones, esta restricción no es necesaria para renderizar el contorno de un trazo.

\ Incluso con esta restricción relajada, las discontinuidades de ángulo de una aproximación de arco son mínimas en comparación con el aplanamiento a líneas. Nuestro enfoque se basa en una métrica de error simple, similar en estilo a la utilizada para aplanar a segmentos de línea. Los detalles de la métrica (en particular, el ajuste de constantes) se obtuvieron empíricamente, aunque sospechamos que se podrían obtener límites analíticos más rigurosos. En la práctica funciona muy bien; la mejor manera de observarlo es mediante una herramienta de prueba interactiva, que se proporciona en los materiales suplementarios.

La métrica de error propuesta es la siguiente. El error de distancia estimado para una curva de longitud 𝑠ˆ es:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Para un segmento de espiral de Euler, 𝜅 ′ (𝑠) es constante y por lo tanto esta métrica de error se vuelve casi trivial. Con 𝑛 subdivisiones, la distancia estimada es simplemente 𝑠 3𝜅 ′ 120𝑛 3 . Resolviendo para 𝑛, obtenemos 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 subdivisiones, y estas se dividen uniformemente por longitud de arco, ya que la densidad de subdivisión es constante a lo largo de la curva, tal como ocurre para aplanar arcos a líneas. Notablemente, la aproximación de una curva paralela de espiral de Euler mediante segmentos de arco es casi tan simple como la de espirales de Euler a arcos.

\ Como en el aplanamiento a líneas, el parámetro para la curva es la longitud de arco de la espiral de Euler original. La densidad de subdivisión es entonces constante, y solo se necesita un pequeño ajuste en la fórmula para calcular el número de subdivisiones, teniendo en cuenta la variación adicional de curvatura del desplazamiento por ℎ (la mitad del ancho de línea). La fórmula revisada es:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Esta fórmula se determinó empíricamente mediante el ajuste de curvas de valores de error medidos al aproximar curvas paralelas de espiral de Euler a arcos, pero también se inspiró en la aplicación de la fórmula general de métrica de error a las ecuaciones analíticas para curvas paralelas de espiral de Euler, y eliminando términos de orden superior. Una derivación más rigurosa, idealmente con límites de error firmes, queda como trabajo futuro.

\ Una consecuencia de esta fórmula es que, dado que el error está en términos del valor absoluto de ℎ, independiente del signo, la misma aproximación de arco puede usarse para ambos lados de un trazo. Vea la Figura 8 para una comparación entre el aplanamiento a una polilínea y la aproximación con segmentos de arco. La versión de segmentos de arco tiene muchos menos segmentos con la misma tolerancia, mientras preserva una calidad visual muy alta.

EVOLUTAS

En la especificación correcta y fundamentada para el trazado [19], las curvas paralelas son suficientes solo para segmentos en los que la curvatura

\

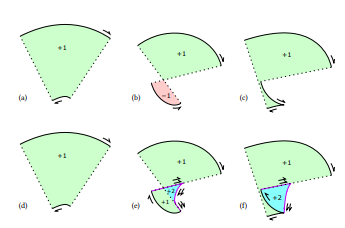
\ no excede el recíproco de la mitad del ancho. Cuando lo hace, se deben dibujar segmentos adicionales, incluidas las evolutas de la curva original. En general, la evoluta de una Bézier cúbica es una curva muy compleja que requiere técnicas de aproximación. Por el contrario, la evoluta de una espiral de Euler (𝜅 = 𝑎𝑠) es otra espiral con una ecuación de Cesàro simple, específicamente 𝜅 = −𝑎 −1 𝑠 −3, un ejemplo del resultado general de que la evoluta de una curva log-estética es otra curva log-estética [26].

\ El aplanamiento de esta evoluta también es sencillo; la densidad de subdivisión es proporcional a 𝑠 −0.5 donde 𝑠 es el parámetro de longitud de arco de la espiral de Euler subyacente (y traducido para que 𝑠 = 0 sea el punto de inflexión). Por lo tanto, la integral es 2 √ 𝑠, y la integral inversa es simplemente elevar al cuadrado. Así, aplanar la evoluta de una espiral de Euler es más simple que aplanar su curva paralela. T

\ el efecto de agregar evolutas para lograr una fuerte corrección se muestra en la Figura 9. Los segmentos adicionales de evoluta y las líneas de conexión se generan dos veces, para hacer que los números de enrollamiento sean consistentes y producir un contorno hermético. Todos los números de enrollamiento son positivos, por lo que el renderizado con la regla de enrollamiento distinto de cero produce un renderizado final correcto.

:::info Autores:

1. Raph Levien
2. Arman Uguray

:::

:::info Este documento está disponible en arxiv bajo licencia CC 4.0.

:::

\