Cómo WormHole acelera la búsqueda de rutas en grafos con miles de millones de aristas

Tabla de Enlaces

Abstracto y 1. Introducción

1.1 Nuestra Contribución

1.2 Configuración

1.3 El algoritmo

1. Trabajo Relacionado

2. Algoritmo

   3.1 La Fase de Descomposición Estructural

   3.2 La Fase de Enrutamiento

   3.3 Variantes de WormHole

3. Análisis Teórico

   4.1 Preliminares

   4.2 Sublinealidad del Anillo Interior

   4.3 Error de Aproximación

   4.4 Complejidad de Consulta

4. Resultados Experimentales

   5.1 WormHole𝐸, WormHole𝐻 y BiBFS

   5.2 Comparación con métodos basados en índices

   5.3 WormHole como primitiva: WormHole𝑀

Referencias

1.1 Nuestra Contribución

Diseñamos un nuevo algoritmo, WormHole, que crea una estructura de datos que nos permite responder a múltiples consultas de caminos más cortos aprovechando la estructura típica de muchas redes sociales y de información. WormHole es simple, fácil de implementar y con respaldo teórico. Proporcionamos varias variantes del mismo, cada una adecuada para un entorno diferente, mostrando excelentes resultados empíricos en una variedad de conjuntos de datos de redes. A continuación se presentan algunas de sus características clave:

\ • Compensación entre rendimiento y precisión. Hasta donde sabemos, el nuestro es el primer algoritmo sublineal aproximado de caminos más cortos en redes grandes. El hecho de que permitamos un pequeño error aditivo da lugar a una compensación entre el tiempo/espacio de preprocesamiento y el tiempo por consulta, y nos permite llegar

\

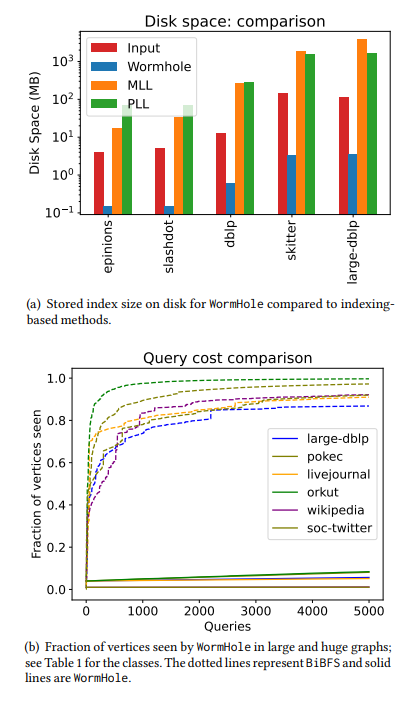
\ a una solución con preprocesamiento eficiente y tiempo rápido por consulta. Notablemente, nuestra variante más precisa (pero más lenta), WormHole𝐸, tiene una precisión casi perfecta: más del 90% de las consultas se responden sin error aditivo, y en todas las redes, más del 99% de las consultas se responden con un error aditivo de como máximo 2. Consulte la Tabla 3 para más detalles.

\ • Tiempo de configuración extremadamente rápido. Nuestro tiempo de construcción de índice más largo fue de solo dos minutos incluso para grafos con miles de millones de aristas. Para contextualizar, PLL y MLL agotaron el tiempo en la mitad de las redes que probamos, y para grafos de tamaño moderado donde PLL y MLL terminaron sus ejecuciones, la construcción del índice WormHole fue 100 veces más rápida. Es decir, WormHole terminó en segundos mientras que PLL tomó horas. Consulte la Tabla 4 y la Tabla 5. Este rápido tiempo de configuración se logra debido al uso de un índice de tamaño sublineal. Para las redes más grandes que consideramos, es suficiente tomar un índice de aproximadamente el 1% de los nodos para obtener un pequeño error aditivo medio – ver Tabla 1. Para redes más pequeñas, puede ser de hasta el 6%.

\ • Tiempo de consulta rápido. En comparación con BiBFS, la versión básica WormHole𝐸 (sin optimizaciones basadas en índices) es 2 veces más rápida para casi todos los grafos y más de 4 veces más rápida en los tres grafos más grandes que probamos. Una variante simple, WormHole𝐻, logra una mejora de un orden de magnitud a costa de cierta precisión: consistentemente 20 veces más rápida en casi todos los grafos, y más de 180 veces para el grafo más grande que tenemos. Consulte la Tabla 3 para una comparación completa. Los métodos basados en indexación típicamente responden consultas en microsegundos; ambas variantes mencionadas anteriormente siguen en el régimen de milisegundos.

\ • Combinando WormHole y el estado del arte. WormHole funciona almacenando un pequeño subconjunto de vértices en los que calculamos los caminos más cortos exactos. Para consultas arbitrarias, enrutamos nuestro camino a través de este subconjunto, que llamamos el núcleo. Utilizamos esta idea para proporcionar una tercera variante, WormHole𝑀, implementando el estado del arte para caminos más cortos, MLL, en el núcleo. Esto logra tiempos de consulta comparables a MLL (con la misma garantía de precisión que WormHole𝐻) a una fracción del costo de configuración, y se ejecuta para grafos masivos donde MLL no termina. Exploramos este enfoque combinado en §5.3, y proporcionamos estadísticas en la Tabla 6.

\ • Complejidad de consulta sublineal. La complejidad de consulta se refiere al número de vértices consultados por el algoritmo. En un modelo de acceso de consulta limitado donde consultar un nodo revela su lista de vecinos (ver §1.2), la complejidad de consulta de nuestro algoritmo escala muy bien con el número de consultas de distancia / camino más corto realizadas. Para responder a 5000 consultas aproximadas de camino más corto, nuestro algoritmo solo observa entre el 1% y el 20% de los nodos para la mayoría de las redes. En comparación, BiBFS ve más del 90% del grafo para responder a unos pocos cientos de consultas de camino más corto. Vea la Figura 2 y la Figura 5 para una comparación.

\ • Garantías demostrables sobre error y rendimiento. En §4 demostramos una serie de resultados teóricos que complementan y explican el rendimiento empírico. Los resultados, enunciados informalmente a continuación, se demuestran para el modelo Chung-Lu de grafos aleatorios con una distribución de grado de ley de potencia [15–17].

\ Teorema 1.1 (Informal). En un grafo aleatorio Chung-Lu 𝐺 con exponente de ley de potencia 𝛽 ∈ (2,3) en 𝑛 vértices, WormHole tiene las siguientes garantías con alta probabilidad:

\

\

:::info Autores:

(1) Talya Eden, Universidad Bar-Ilan (talyaa01@gmail.com);

(2) Omri Ben-Eliezer, MIT (omrib@mit.edu);

(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).

:::

:::info Este artículo está disponible en arxiv bajo licencia CC BY 4.0.

:::

\