Une formule plus simple pour l'approximation de courbe utilisant des segments d'arc

Table Des Liens

RÉSUMÉ

1 INTRODUCTION

2 APLATISSEMENT ET APPROXIMATION D'ARC DES COURBES

3 SPIRALES D'EULER ET LEURS COURBES PARALLÈLES

4 COURBES PARALLÈLES APLATIES

5 MÉTRIQUES D'ERREUR POUR L'APPROXIMATION PAR ARCS

6 DÉVELOPPÉES

7 CONVERSION DES BÉZIERS CUBIQUES EN SPIRALES D'EULER

8 IMPLÉMENTATION GPU

9 RÉSULTATS

CONCLUSIONS, TRAVAUX FUTURS ET RÉFÉRENCES

\

MÉTRIQUES D'ERREUR POUR L'APPROXIMATION PAR ARCS

Le problème d'approximation d'une courbe par une séquence de segments d'arc fait l'objet d'une littérature abondante, mais aucune des solutions publiées n'est vraiment adaptée à notre application. Le problème spécifique de l'approximation d'une spirale d'Euler par des arcs est considéré dans Meek et Walton [2004] utilisant un schéma de subdivision adaptative "couper puis mesurer", mais leur solution est de mauvaise qualité ; elle évolue en 𝑂(1/𝑛 2 ), alors que 𝑂(1/𝑛 3 ) est réalisable. Le résultat a été amélioré "légèrement" par Narayan [2014].

\ La littérature contient également des résultats optimaux, notamment Maier [2014] et Nuntawisuttiwong et Dejdumrong [2021], mais à un coût considérable ; les deux approches revendiquent une complexité temporelle de 𝑂(𝑛 2 ). Le fil conducteur de tous ces résultats est qu'ils résolvent un problème plus difficile : adopter la contrainte que la séquence d'arcs générée est continue 𝐺 1 . Bien que souhaitable pour de nombreuses applications, cette contrainte n'est pas nécessaire pour le rendu d'un contour de trait.

\ Même avec cette contrainte assouplie, les discontinuités d'angle d'une approximation d'arc sont minimes par rapport à l'aplatissement en lignes. Notre approche est basée sur une métrique d'erreur simple, similaire à celle utilisée pour l'aplatissement en segments de ligne. Les détails de la métrique (en particulier, l'ajustement des constantes) ont été obtenus empiriquement, bien que nous soupçonnions que des limites analytiques plus rigoureuses pourraient être obtenues. En pratique, cela fonctionne très bien ; la meilleure façon de l'observer est un outil de test interactif, qui est fourni dans les matériaux supplémentaires.

La métrique d'erreur proposée est la suivante. L'erreur de distance estimée pour une courbe de longueur 𝑠ˆ est :

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Pour un segment de spirale d'Euler, 𝜅 ′ (𝑠) est constant et donc cette métrique d'erreur devient presque triviale. Avec 𝑛 subdivisions, la distance estimée est simplement 𝑠 3𝜅 ′ 120𝑛 3 . En résolvant pour 𝑛, nous obtenons 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 subdivisions, et celles-ci sont réparties uniformément par longueur d'arc, car la densité de subdivision est constante sur toute la courbe, comme c'est le cas pour l'aplatissement des arcs en lignes. Remarquablement, l'approximation d'une courbe parallèle à une spirale d'Euler par des segments d'arc est presque aussi simple que celle des spirales d'Euler en arcs.

\ Comme dans l'aplatissement en lignes, le paramètre pour la courbe est la longueur d'arc de la spirale d'Euler d'origine. La densité de subdivision est alors constante, et seule une petite modification est nécessaire à la formule pour calculer le nombre de subdivisions, en tenant compte de la variation de courbure supplémentaire due au décalage par ℎ (la demi-largeur de ligne). La formule révisée est :

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Cette formule a été déterminée empiriquement par ajustement de courbe des valeurs d'erreur mesurées lors de l'approximation des courbes parallèles à la spirale d'Euler en arcs, mais a également été inspirée par l'application de la formule de métrique d'erreur générale aux équations analytiques pour la courbe parallèle à la spirale d'Euler, en abandonnant les termes d'ordre supérieur. Une dérivation plus rigoureuse, idéalement avec des limites d'erreur fermes, reste un travail futur.

\ Une conséquence de cette formule est que, puisque l'erreur est exprimée en termes de valeur absolue de ℎ, indépendamment du signe, la même approximation d'arc peut être utilisée pour les deux côtés d'un trait. Voir la Figure 8 pour une comparaison entre l'aplatissement en polyligne et l'approximation avec des segments d'arc. La version avec segments d'arc a beaucoup moins de segments à la même tolérance, tout en préservant une très haute qualité visuelle.

DÉVELOPPÉES

Dans la spécification correcte et rigoureuse pour le tracé [19], les courbes parallèles ne sont suffisantes que pour les segments dans lesquels la courbure

\

\ ne dépasse pas la demi-largeur réciproque. Lorsqu'elle le fait, des segments supplémentaires doivent être dessinés, y compris les développées de la courbe originale. En général, la développée d'une Bézier cubique est une courbe très complexe, nécessitant des techniques d'approximation. En revanche, la développée d'une spirale d'Euler (𝜅 = 𝑎𝑠) est une autre spirale avec une équation de Cesàro simple, à savoir 𝜅 = −𝑎 −1 𝑠 −3 , un exemple du résultat général selon lequel la développée d'une courbe log-esthétique est une autre courbe log-esthétique [26].

\ L'aplatissement de cette développée est également simple ; la densité de subdivision est proportionnelle à 𝑠 −0.5 où 𝑠 est le paramètre de longueur d'arc de la spirale d'Euler sous-jacente (et traduit de sorte que 𝑠 = 0 est le point d'inflexion). Ainsi, l'intégrale est 2 √ 𝑠, et l'intégrale inverse est simplement l'élévation au carré. Ainsi, l'aplatissement de la développée d'une spirale d'Euler est plus simple que l'aplatissement de sa courbe parallèle. L

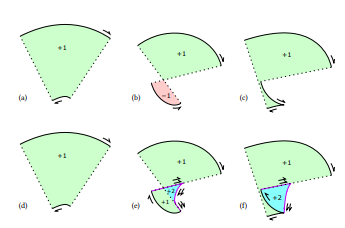
\ 'effet de l'ajout de développées pour atteindre une forte correction est montré dans la Figure 9. Les segments de développée supplémentaires et les lignes de connexion sont produits deux fois, pour rendre les nombres d'enroulement cohérents et produire un contour étanche. Tous les nombres d'enroulement sont positifs, donc le rendu avec la règle de nombre d'enroulement non nul donne un rendu final correct.

:::info Auteurs :

1. Raph Levien
2. Arman Uguray

:::

:::info Cet article est disponible sur arxiv sous licence CC 4.0.

:::

\