Les fractales sont des motifs sans fin créés par la répétition d'équations mathématiques. Nous allons dessiner l'une des fractales les plus connues, en utilisant uniquement du JavaScript Vanilla et l'API Canvas HTML5.Les fractales sont des motifs sans fin créés par la répétition d'équations mathématiques. Nous allons dessiner l'une des fractales les plus connues, en utilisant uniquement du JavaScript Vanilla et l'API Canvas HTML5.

Coder un Arbre Fractal Avec JavaScript et HTML5

Par : Hackernoon

2025/10/11 03:00

TREE$0.1205+1.85%

LL$0.007927-0.07%

\ Les fractales, ces figures énigmatiques qui sont partout mais ne peuvent être vues par un œil non exercé. Aujourd'hui, nous allons dessiner l'une des fractales les plus connues, en utilisant uniquement du JavaScript Vanilla et l'API Canvas HTML5. Commençons à coder !

Ce que vous allez apprendre

Qu'est-ce qu'un arbre fractal ?
Écrire l'arbre fractal en JavaScript Vanilla
Au-delà de l'arbre fractal

Qu'est-ce qu'un arbre fractal ?

Pour définir un arbre fractal, nous devons d'abord connaître la définition d'une fractale, bien sûr.

Les fractales sont des motifs sans fin créés par la répétition d'équations mathématiques qui, à n'importe quelle échelle, à n'importe quel niveau de zoom, semblent à peu près identiques. En d'autres termes, un objet géométrique dont la structure de base, rugueuse ou fragmentée, se répète à différentes échelles.

Donc si nous divisons une fractale, nous verrons une copie réduite de l'ensemble.

Benoit Mandelbrot, qui a inventé le terme fractale en 1975, a dit :

\ Assez clair, n'est-ce pas ?

Voici quelques exemples :

Courbe de Von Koch animée

\ Tapis de Sierpinski animé

Maintenant, qu'est-ce qu'un arbre fractal ?

Imaginez une branche, et des branches qui en sortent, puis deux branches qui sortent de chaque branche, et ainsi de suite... c'est à quoi ressemble un arbre fractal.

Sa forme provient du triangle de Sierpinski (ou joint de Sierpinski).

Comme vous pouvez le voir, l'un devient l'autre en changeant l'angle entre les branches :

$Du triangle de Sierpinski à la fractale$

Aujourd'hui, nous finirons avec une figure similaire à la forme finale de ce GIF.

Écrire l'arbre fractal en JavaScript Vanilla

Tout d'abord, voici le produit final (vous pouvez le modifier en cours de route) :

$Arbre fractal final$

Maintenant, dessinons cela, étape par étape.

Tout d'abord, nous initialisons notre fichier index.html avec un canvas de dimensions raisonnables et une balise script où tout notre code JS sera placé.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

Ensuite, nous commençons à écrire notre JavaScript.

Nous initialisons notre élément canvas en JS, en y accédant via la variable myCanvas et en créant le contexte de rendu 2D avec la variable ctx (contexte).

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

Donc oui, la méthode getContext ajoute des propriétés et des méthodes qui vous permettent de dessiner, dans ce cas, en 2D.

Maintenant, il est temps de réfléchir. Comment pouvons-nous définir l'algorithme pour dessiner un arbre fractal ? Hm... 🤔

Voyons voir, nous savons que les branches deviennent de plus en plus petites. Et que chaque branche se termine par deux branches qui en sortent, une à gauche et une à droite.

En d'autres termes, lorsqu'une branche est assez longue, attachez-y deux branches plus petites. Répétez.

Cela ressemble à l'utilisation d'une instruction récursive quelque part, n'est-ce pas ?

Revenons au code, nous définissons maintenant notre fonction fractalTree qui devrait prendre au moins quatre arguments : les coordonnées X et Y où commence la branche, la longueur de sa branche et son angle.

Dans notre fonction, nous commençons le dessin avec la méthode beginPath(), puis nous sauvegardons l'état du canvas avec la méthode save().

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

La méthode beginPath est souvent utilisée lorsque vous commencez une nouvelle ligne ou figure qui a un style fixe, comme la même couleur tout au long de la ligne, ou la même largeur. La méthode save sauvegarde simplement l'état entier du canvas en poussant l'état actuel sur une pile.

Maintenant, nous allons dessiner notre arbre fractal en traçant une ligne (branche), en faisant pivoter le canvas, en dessinant la branche suivante, et ainsi de suite. Cela se passe comme ceci (j'expliquerai chaque méthode sous l'exemple de code) :

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

Nous ajoutons d'abord trois méthodes, translate, rotate et moveTo, qui "déplacent" le canvas, son origine et notre "crayon" afin que nous puissions dessiner la branche dans l'angle souhaité. C'est comme si nous dessinions une branche, puis centrions cette branche (en déplaçant tout le canvas), puis dessinions une nouvelle branche à partir de l'extrémité de notre branche précédente.

Les deux dernières méthodes avant l'instruction if sont lineTo et stroke ; la première ajoute une ligne droite au chemin actuel, et la seconde la rend. Vous pouvez voir cela comme ceci : lineTo donne l'ordre, et stroke l'exécute.

Maintenant, nous avons une instruction if qui indique quand arrêter la récursion, quand arrêter de dessiner. La méthode restore, comme indiqué dans la documentation MDN, "restaure l'état du canvas le plus récemment sauvegardé en retirant l'entrée supérieure de la pile d'état de dessin".

Après l'instruction if, nous avons l'appel récursif et un autre appel à la méthode restore. Et ensuite un appel à la fonction que nous venons de terminer.

Maintenant, exécutez le code dans votre navigateur. Vous verrez, enfin, un arbre fractal !

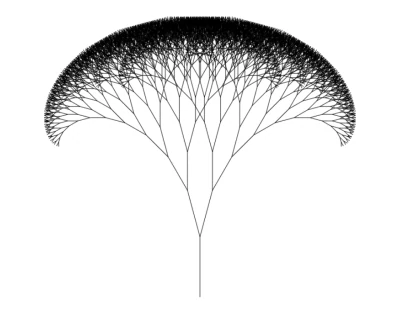
$Première itération de l'arbre fractal$

Génial, n'est-ce pas ? Maintenant, rendons-le encore meilleur.

Nous allons ajouter un nouveau paramètre à notre fonction draw, branchWidth, pour rendre notre arbre fractal plus réaliste.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Donc à chaque itération, nous rendons chaque branche plus fine. J'ai également modifié le paramètre d'angle dans l'appel récursif pour créer un arbre plus "ouvert".

Maintenant, ajoutons de la couleur ! Et des ombres, pourquoi pas.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.strokeStyle = "green";           ctx.fillStyle = "green";            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            ctx.shadowBlur = 15;           ctx.shadowColor = "rgba(0,0,0,0.8)";            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Les deux méthodes de couleur sont explicites (strokeStyle et fillStyle). De même pour celles des ombres, shadowBlur et shadowColor.

Et c'est tout ! Sauvegardez le fichier et ouvrez-le avec votre navigateur pour voir le produit final.

Maintenant, je vous encourage à jouer avec le code ! Changez la shadowColor, le fillStyle, faites un arbre fractal plus court ou plus long, changez l'angle, ou essayez d'ajouter des feuilles, ce qui devrait être un défi 😉

Au-delà de l'arbre fractal

Comme je vous l'ai montré au début de cet article, il existe différentes fractales. Ce ne sera pas facile de toutes les réaliser avec l'API Canvas, mais cela devrait être possible. J'en ai réalisé certaines dans le langage de programmation C, et j'ai également expérimenté avec p5.js.

p5.js est une bibliothèque JavaScript Open Source créée par des artistes, pour des artistes, basée sur le langage Processing. Vous pouvez dessiner ou animer tout ce que vous pouvez imaginer. Si vous êtes intéressé par la création d'art avec du code, c'est un incontournable. Ils ont une excellente page get-started que vous pouvez consulter ici.

Clause de non-responsabilité : les articles republiés sur ce site proviennent de plateformes publiques et sont fournis à titre informatif uniquement. Ils ne reflètent pas nécessairement les opinions de MEXC. Tous les droits restent la propriété des auteurs d'origine. Si vous estimez qu'un contenu porte atteinte aux droits d'un tiers, veuillez contacter service@support.mexc.com pour demander sa suppression. MEXC ne garantit ni l'exactitude, ni l'exhaustivité, ni l'actualité des contenus, et décline toute responsabilité quant aux actions entreprises sur la base des informations fournies. Ces contenus ne constituent pas des conseils financiers, juridiques ou professionnels, et ne doivent pas être interprétés comme une recommandation ou une approbation de la part de MEXC.