educe Truth Bias and Speed Up Unfolding with Moment‑Conditioned Diffusion
Table of Links
Abstract and 1. Introduction
-
Unfolding
2.1 Posing the Unfolding Problem
2.2 Our Unfolding Approach
-
Denoising Diffusion Probabilistic Models
3.1 Conditional DDPM
-
Unfolding with cDDPMs
-
Results
5.1 Toy models
5.2 Physics Results
-
Discussion, Acknowledgments, and References
\ Appendices
A. Conditional DDPM Loss Derivation
B. Physics Simulations
C. Detector Simulation and Jet Matching
D. Toy Model Results
E. Complete Physics Results
3 Denoising Diffusion Probabilistic Models

\ By learning to reverse the forward diffusion process, the model learns meaningful latent representations of the underlying data and is able to remove noise from data to generate new samples from the associated data distribution. This type of generative model has natural applications in high energy physics, for example generating data samples from known particle distributions. However, to be used in unfolding the process must be altered so that the denoising procedure is dependent on the observed detector data, y. This can be achieved by incorporating conditioning methods to the DDPM
\
3.1 Conditional DDPM
Conditioning methods for DDPMs can either use conditions to guide unconditional DDPMs in the reverse process [7], or they can incorporate direct conditions to the learned reverse process. While guided diffusion methods have had great success in image synthesis [10], direct conditioning provides a framework that is particularly useful in unfolding.
\ We implement a conditional DDPM (cDDPM) for unfolding that keeps the original unconditional forward process and introduces a simple, direct conditioning on y to the reverse process,
\ \ 
\ \ This conditioned reverse process learns to directly estimate the posterior probability P(x|y) through its Gaussian transitions. More specifically, the reverse process, parameterized by θ, learns to remove the introduced noise to recover the target value x by conditioning directly on y
\ \ 
\
4 Unfolding with cDDPMs
\ 
\
4.1 Multidimensional Particle-Wise Unfolding
\ 
\
4.2 Generalization and Inductive Bias
\ 
\
5 Results
5.1 Toy models
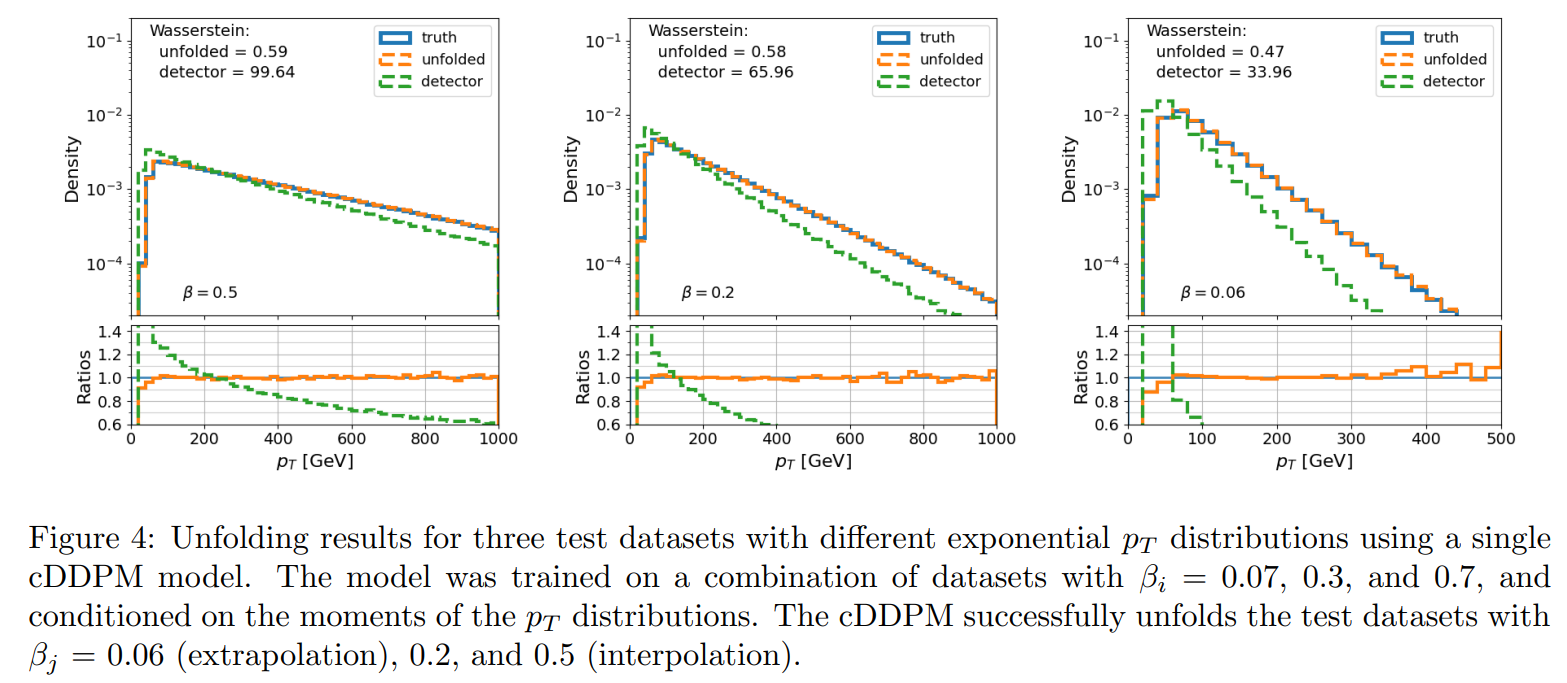
Proof-of-concept was demonstrated using toy models with non-physics data. To evaluate the unfolding performance, we calculated the 1-dimensional Wasserstein and Energy distances between the truth-level, unfolded, and detector-level data for each component in the data vectors of the samples. We also computed the Wasserstein distance and KL divergence between the histograms of the truth-level data and those of the
\ 

\ 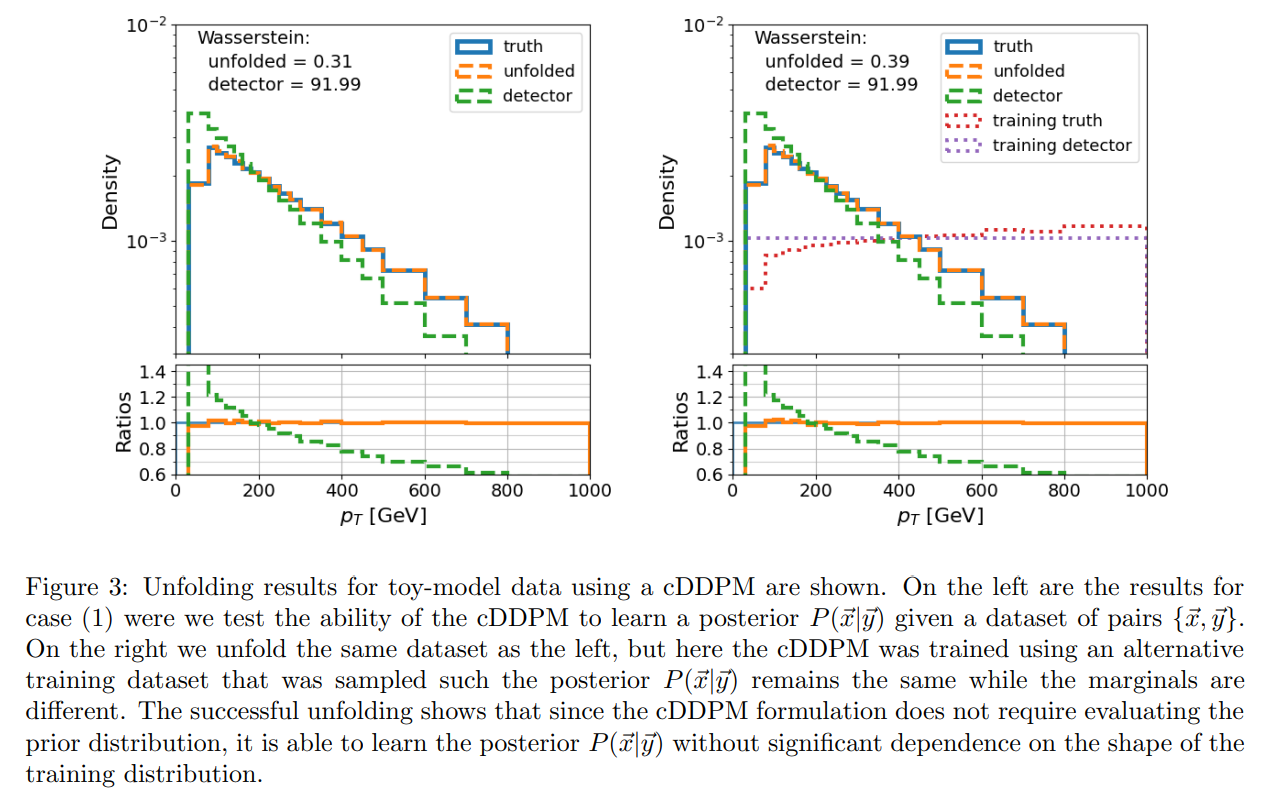
\ unfolded and detector-level data. The sample-based Wasserstein distances are displayed on each plot, and a comprehensive list of the metrics is provided in appendix D.
\ 
\ 
\ 
\
5.2 Physics Results
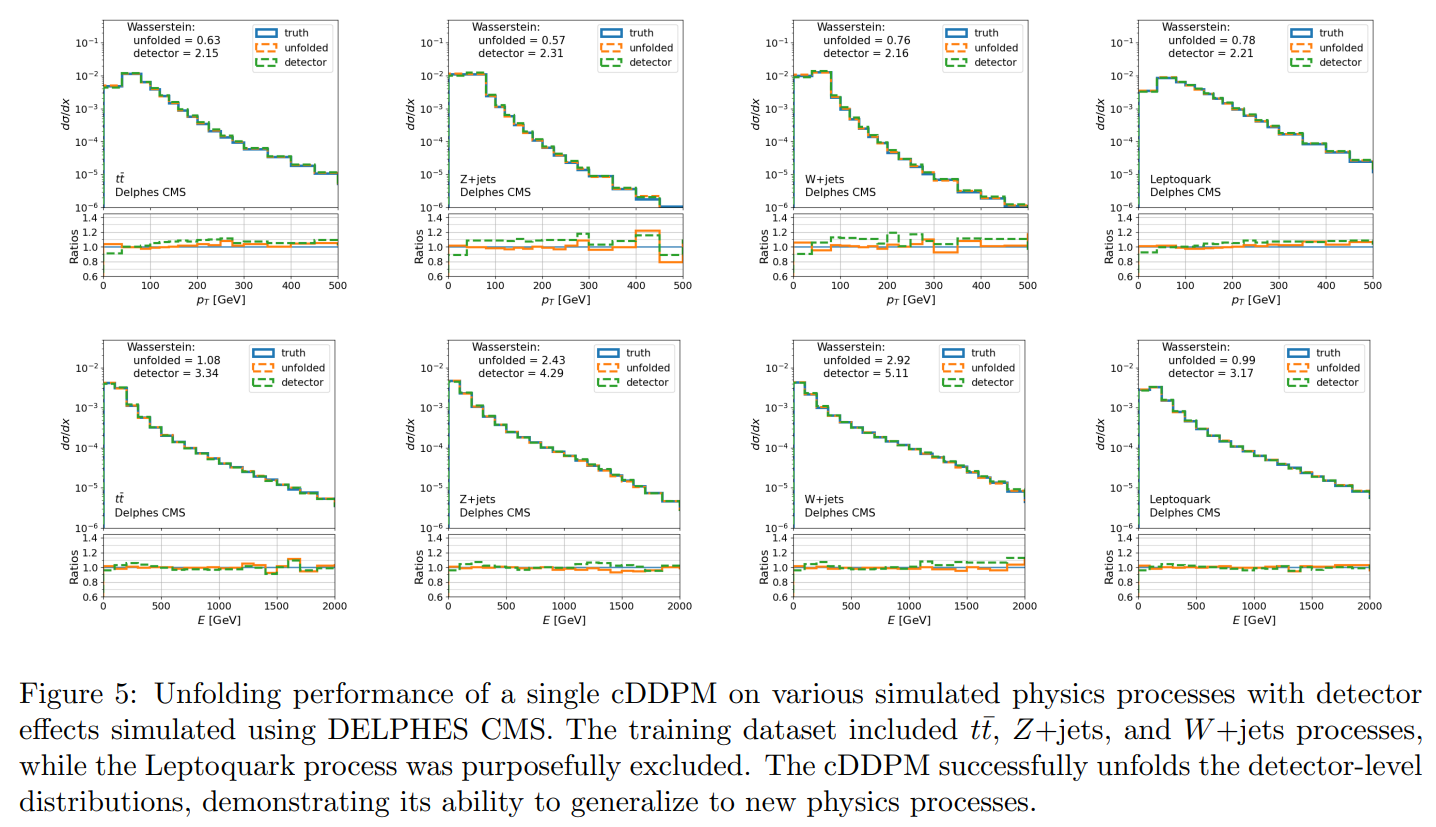
We test our approach on particle physics data by applying it to jet datasets from various processes sampled using the PYTHIA event generator (details of these synthetic datasets can be found in appendix B). The generated truth-level jets were passed through two different detector simulation frameworks to simulate particle interactions within an LHC detector. The detector simulations used were DELPHES with the standard CMS configuration, and another detector simulator developed using an analytical data-driven approximation for the pT , η, and ϕ resolutions from results published by the ATLAS collaboration (more details in appendix C). The DELPHES CMS detector simulation is the standard and allows comparison to other machine-learning based unfolding algorithms, while the data-driven detector simulation tests the unfolding success under more drastic detector smearing.
\ 
\ 
\
:::info Authors:
(1) Camila Pazos, Department of Physics and Astronomy, Tufts University, Medford, Massachusetts;
(2) Shuchin Aeron, Department of Electrical and Computer Engineering, Tufts University, Medford, Massachusetts and The NSF AI Institute for Artificial Intelligence and Fundamental Interactions;
(3) Pierre-Hugues Beauchemin, Department of Physics and Astronomy, Tufts University, Medford, Massachusetts and The NSF AI Institute for Artificial Intelligence and Fundamental Interactions;
(4) Vincent Croft, Leiden Institute for Advanced Computer Science LIACS, Leiden University, The Netherlands;
(5) Martin Klassen, Department of Physics and Astronomy, Tufts University, Medford, Massachusetts;
(6) Taritree Wongjirad, Department of Physics and Astronomy, Tufts University, Medford, Massachusetts and The NSF AI Institute for Artificial Intelligence and Fundamental Interactions.
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
Vous aimerez peut-être aussi

Microsoft reportedly ready to abandon high-stakes talks with OpenAI

Ethereum ETF Inflows Hit Record Highs, Will It Kick Off the Alt Season?
