Toto如何重新构想多头注意力机制用于多变量预测

链接表

1. 背景
2. 问题陈述
3. 模型架构
4. 训练数据
5. 结果
6. 结论
7. 影响声明
8. 未来方向
9. 贡献
10. 致谢和参考文献

附录

3 模型架构

Toto是一个仅解码器的预测模型。该模型采用了文献中的许多最新技术，并引入了一种新方法来使多头注意力适应多变量时间序列数据（图1）。

\ 3.1 Transformer设计

\ 用于时间序列预测的Transformer模型已经使用了各种编码器-解码器[12, 13, 21]、仅编码器[14, 15, 17]和仅解码器架构[19, 23]。对于Toto，我们采用仅解码器架构。解码器架构已被证明可以很好地扩展[25, 26]，并允许任意预测范围。因果下一块预测任务也简化了预训练过程。

\ 我们使用了一些最新的大型语言模型（LLM）架构中的技术，包括预归一化[27]、RMSNorm[28]和SwiGLU前馈层[29]。

\ 3.2 输入嵌入

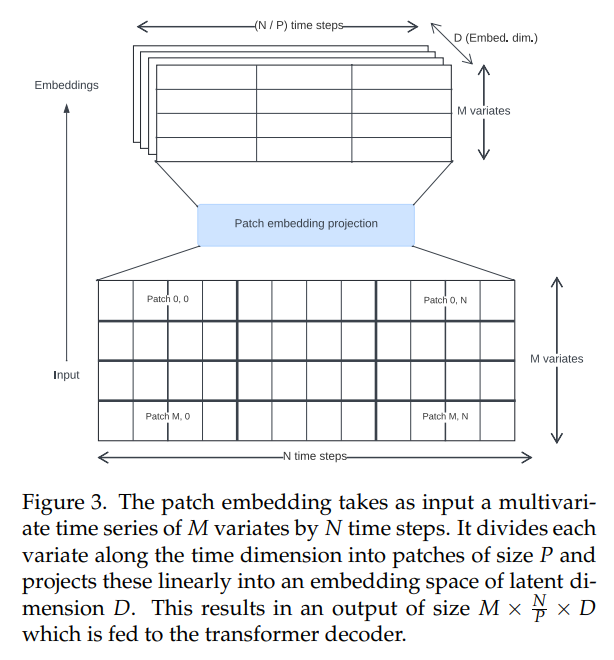
\ 文献中的时间序列transformer使用了各种方法来创建输入嵌入。我们使用非重叠块投影（图3），这最初是为Vision Transformers[30, 31]引入的，并在时间序列上下文中由PatchTST[14]推广。Toto使用固定块大小32进行训练。

\

\ 3.3 注意力机制

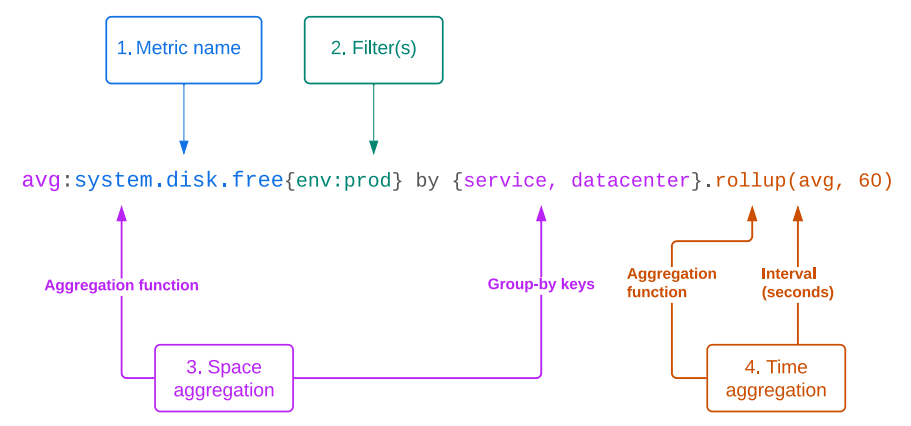
\ 可观测性指标通常是高基数、多变量时间序列。因此，理想的模型将原生处理多变量预测。它应该能够分析时间维度（我们称之为"时间方向"交互）和通道维度（我们称之为"空间方向"交互，遵循Datadog平台中将指标的不同组或标签集描述为"空间"维度的惯例）中的关系。

\ 为了同时建模空间和时间方向的交互，我们需要将传统的多头注意力架构[11]从一维适应到二维。文献中已经提出了几种方法来实现这一点，包括：

\ • 假设通道独立，并且只在时间维度上计算注意力[14]。这是高效的，但丢弃了所有关于空间方向交互的信息。

\ • 仅在空间维度上计算注意力，并在时间维度上使用前馈网络[17, 18]。

\ • 沿时间维度连接变量并计算每个空间/时间位置之间的完全交叉注意力[15]。这可以捕获每一个可能的空间和时间交互，但计算成本很高。

\ • 计算"因子化注意力"，其中每个transformer块包含单独的空间和时间注意力计算[16, 32, 33]。这允许空间和时间混合，并且比完全交叉注意力更高效。然而，它使网络的有效深度加倍。

\ 为了设计我们的注意力机制，我们遵循这样的直觉：对于许多时间序列，时间关系比空间关系更重要或更具预测性。作为证据，我们观察到即使完全忽略空间方向关系的模型（如PatchTST[14]和TimesFM[19]）仍然可以在多变量数据集上取得有竞争力的性能。然而，其他研究（例如Moirai[15]）通过消融实验表明，包含空间方向关系确实有一些明显的好处。

\ 因此，我们提出了一种因子化注意力的新变体，我们称之为"比例因子化空间-时间注意力"。我们使用交替的空间方向和时间方向注意力块的混合。作为可配置的超参数，我们可以改变时间方向与空间方向块的比例，从而允许我们为每种类型的注意力分配更多或更少的计算预算。对于我们的基本模型，我们选择了每两个时间方向块配置一个空间方向注意力块。

\ 在时间方向注意力块中，我们使用因果掩码和旋转位置嵌入[34]与XPOS[35]，以自回归方式建模时间依赖特征。相比之下，在空间方向块中，我们使用完全双向注意力以保持协变量的排列不变性，并使用块对角ID掩码确保只有相关变量相互关注。这种掩码允许我们将多个独立的多变量时间序列打包到同一批次中，以提高训练效率并减少填充量。

\ 3.4 概率预测头

\ 为了在预测应用中有用，模型应该产生概率预测。时间序列模型中的一种常见做法是使用输出层，其中模型回归概率分布的参数。这允许使用蒙特卡洛采样[7]计算预测区间。

\ 输出层的常见选择是正态分布[7]和学生T分布[23, 36]，这可以提高对异常值的鲁棒性。Moirai[15]通过提出一种新的混合模型，结合了高斯分布、学生T分布、对数正态分布和负二项分布输出的加权组合，允许更灵活的残差分布。

\ 然而，现实世界的时间序列通常具有复杂的分布，这些分布具有异常值、重尾、极端偏斜和多模态，难以拟合。为了适应这些情况，我们引入了更灵活的输出似然。为此，我们采用基于高斯混合模型（GMMs）的方法，它可以近似任何密度函数（[37]）。为了避免在存在异常值时的训练不稳定，我们使用学生T混合模型（SMM），这是GMMs的一种鲁棒泛化[38]，之前已经显示出对建模重尾金融时间序列的前景[39, 40]。该模型预测每个时间步的k个学生T分布（其中k是一个超参数），以及学习的权重。

\

\ 当我们执行推理时，我们在每个时间戳从混合分布中抽取样本，然后将每个样本反馈到解码器中进行下一个预测。这使我们能够在任何分位数生成预测区间，仅受样本数量的限制；对于更精确的尾部，我们可以选择在采样上花费更多的计算（图2）。

\ 3.5 输入/输出缩放

\ 与其他时间序列模型一样，我们在将输入数据通过块嵌入之前对其执行实例归一化，以使模型更好地泛化到不同尺度的输入[41]。我们将输入缩放为零均值和单位标准差。然后将输出预测重新缩放回原始单位。

\ 3.6 训练目标

\ 作为仅解码器模型，Toto在下一块预测任务上进行预训练。我们最小化下一个预测块相对于模型分布输出的负对数似然。我们使用AdamW优化器[42]训练模型。

\ 3.7 超参数

\ Toto使用的超参数详见表A.1，总共有1.03亿个参数。

\

:::info 作者：

(1) Ben Cohen (ben.cohen@datadoghq.com);

(2) Emaad Khwaja (emaad@datadoghq.com);

(3) Kan Wang (kan.wang@datadoghq.com);

(4) Charles Masson (charles.masson@datadoghq.com);

(5) Elise Rame (elise.rame@datadoghq.com);

(6) Youssef Doubli (youssef.doubli@datadoghq.com);

(7) Othmane Abou-Amal (othmane@datadoghq.com).

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0许可。

:::

\