صيغة أبسط لتقريب المنحنى باستخدام قطاعات القوس

جدول الروابط

الملخص

1 المقدمة

2 تسطيح وتقريب الأقواس للمنحنيات

3 حلزونات أويلر ومنحنياتها المتوازية

4 المنحنيات المتوازية المسطحة

5 مقاييس الخطأ للتقريب بالأقواس

6 المنحنيات المتطورة

7 التحويل من منحنيات بيزييه التكعيبية إلى حلزونات أويلر

8 تنفيذ وحدة معالجة الرسومات

9 النتائج

الاستنتاجات، العمل المستقبلي والمراجع

\

مقاييس الخطأ للتقريب بالأقواس

تحظى مشكلة تقريب منحنى بسلسلة من قطاعات الأقواس بأدبيات واسعة، لكن أياً من الحلول المنشورة ليست مناسبة تماماً لتطبيقنا. تمت دراسة المشكلة المحددة لتقريب حلزون أويلر بالأقواس في دراسة ميك ووالتون [2004] باستخدام مخطط تقسيم فرعي تكيفي "قطع ثم قياس"، لكن حلهم كان ذا جودة منخفضة؛ حيث يتدرج بمقياس 𝑂(1/𝑛 2 )، بينما يمكن تحقيق 𝑂(1/𝑛 3 ). تم تحسين النتيجة "قليلاً" بواسطة نارايان [2014].

\ تحتوي الأدبيات أيضاً على نتائج مثالية، وتحديداً ماير [2014] ونونتاويسوتيونج وديجدومرونج [2021]، ولكن بتكلفة كبيرة؛ حيث يدعي كلا النهجين تعقيداً زمنياً قدره 𝑂(𝑛 2 ). الخط المشترك لجميع هذه النتائج هو أنها تحل مشكلة أصعب: تبني القيد بأن تسلسل الأقواس المُنشأ هو مستمر 𝐺 1. على الرغم من أن هذا القيد مرغوب فيه للعديد من التطبيقات، إلا أنه غير مطلوب لعرض مخطط الخط.

\ حتى مع تخفيف هذا القيد، فإن انقطاعات الزاوية لتقريب القوس ضئيلة مقارنة بالتسطيح إلى خطوط. يعتمد نهجنا على مقياس خطأ بسيط، مشابه في طابعه للمقياس المستخدم لتسطيح قطاعات الخط. تم الحصول على تفاصيل المقياس (وخاصة ضبط الثوابت) بشكل تجريبي، على الرغم من أننا نشك في إمكانية الحصول على حدود تحليلية أكثر صرامة. في الممارسة العملية، يعمل بشكل جيد جداً؛ وأفضل طريقة لملاحظة ذلك هي أداة اختبار تفاعلية، والتي يتم توفيرها في المواد التكميلية.

مقياس الخطأ المقترح هو كما يلي. خطأ المسافة المقدرة لمنحنى بطول 𝑠ˆ هو:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

بالنسبة لقطعة حلزون أويلر، فإن 𝜅 ′ (𝑠) ثابتة وبالتالي يصبح مقياس الخطأ هذا بسيطاً تقريباً. مع 𝑛 من التقسيمات الفرعية، تكون المسافة المقدرة ببساطة 𝑠 3𝜅 ′ 120𝑛 3. بحل المعادلة لـ 𝑛، نحصل على 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 تقسيمات فرعية، ويتم تقسيمها بالتساوي حسب طول القوس، حيث تكون كثافة التقسيم الفرعي ثابتة عبر المنحنى، تماماً كما هو الحال بالنسبة لتسطيح الأقواس إلى خطوط. من الملاحظ أن تقريب منحنى متوازٍ لحلزون أويلر بواسطة قطاعات قوسية هو تقريباً بنفس بساطة تقريب حلزونات أويلر إلى أقواس.

\ كما هو الحال في التسطيح إلى خطوط، فإن المعلمة للمنحنى هي طول القوس لحلزون أويلر الأصلي. تكون كثافة التقسيم الفرعي ثابتة، ويلزم فقط تعديل صغير للصيغة لحساب عدد التقسيمات الفرعية، مع الأخذ في الاعتبار التباين الإضافي في الانحناء من الإزاحة بواسطة ℎ (نصف عرض الخط). الصيغة المعدلة هي:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

تم تحديد هذه الصيغة تجريبياً من خلال ملاءمة المنحنى لقيم الخطأ المقاسة من تقريب منحنيات متوازية لحلزون أويلر إلى أقواس، ولكنها استوحيت أيضاً من تطبيق صيغة مقياس الخطأ العامة على المعادلات التحليلية لمنحنى متوازٍ لحلزون أويلر، وإسقاط الحدود ذات الرتبة الأعلى. لا يزال اشتقاق أكثر صرامة، مثالياً مع حدود خطأ ثابتة، عملاً مستقبلياً.

\ إحدى نتائج هذه الصيغة هي أنه، نظراً لأن الخطأ يكون من حيث القيمة المطلقة لـ ℎ، بغض النظر عن الإشارة، يمكن استخدام نفس تقريب القوس لكلا جانبي الخط. انظر الشكل 8 للمقارنة بين التسطيح إلى خط متعدد الأضلاع والتقريب بقطاعات قوسية. إصدار قطاع القوس يحتوي على عدد أقل بكثير من القطاعات عند نفس التفاوت، مع الحفاظ على جودة بصرية عالية جداً.

المنحنيات المتطورة

في المواصفات المبدئية الصحيحة للتخطيط [19]، تكون المنحنيات المتوازية كافية فقط للقطاعات التي يكون فيها الانحناء

\

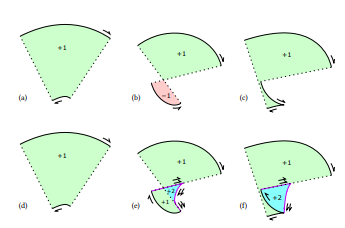
\ لا يتجاوز مقلوب نصف العرض. عندما يحدث ذلك، يجب رسم قطاعات إضافية، بما في ذلك المنحنيات المتطورة للمنحنى الأصلي. بشكل عام، المنحنى المتطور لمنحنى بيزييه التكعيبي هو منحنى معقد للغاية، يتطلب تقنيات تقريبية. على النقيض من ذلك، فإن المنحنى المتطور لحلزون أويلر (𝜅 = 𝑎𝑠) هو حلزون آخر بمعادلة سيزارو بسيطة، وهي 𝜅 = −𝑎 −1 𝑠 −3، وهي حالة من النتيجة العامة التي تفيد بأن المنحنى المتطور لمنحنى جمالي لوغاريتمي هو منحنى جمالي لوغاريتمي آخر [26].

\ تسطيح هذا المنحنى المتطور أمر بسيط أيضاً؛ كثافة التقسيم الفرعي تتناسب مع 𝑠 −0.5 حيث 𝑠 هي معلمة طول القوس لحلزون أويلر الأساسي (وتُترجم بحيث تكون 𝑠 = 0 هي نقطة الانعطاف). وبالتالي، فإن التكامل هو 2 √ 𝑠، والتكامل العكسي هو مجرد تربيع. وبالتالي، فإن تسطيح المنحنى المتطور لحلزون أويلر أبسط من تسطيح منحناه المتوازي. ت

\ أثير إضافة المنحنيات المتطورة لتحقيق الصحة القوية موضح في الشكل 9. يتم إخراج قطاعات المنحنى المتطور الإضافية والخطوط الموصلة مرتين، لجعل أرقام اللف متسقة وإنتاج مخطط محكم. جميع أرقام اللف موجبة، لذا فإن العرض باستخدام قاعدة اللف غير الصفرية ينتج عرضاً نهائياً صحيحاً.

:::info المؤلفون:

1. راف ليفين
2. أرمان أوغوراي

:::

:::info هذه الورقة متاحة على arxiv تحت ترخيص CC 4.0.

:::

\