全像傳播子:測地線與局部臨界性
連結表
- 序言
- 圖解規則
- 直接艾康納爾方法
- 傳統玻色化
- 餛飩全息
- 全息傳播子
- 奇異銅酸鹽
- 更奇異的事物
- 尾聲
全息傳播子
早期關於費米子傳播子的全息研究[28]產生了許多引人入勝的結果,包括多重費米面(在某些極端情況下合併為一個臨界「費米球」)、無色散極點,以及振盪頻率依賴性(後來被證明在更系統性的「自上而下」構建[26]中不會出現)等。這些結果的物理解釋受到阻礙,因為大部分工作都是數值計算。
\ 在 mL ≫ 1 的區域中可以進行簡單且適合解析處理的半經典計算,其中 m 是推測的對偶體積費米子的質量[28, 29]。在這個區域中,費米子路徑對各種量子力學振幅的貢獻緊密遵循從(虛時間)作用量導出的經典邊界到邊界軌跡(測地線)
\ 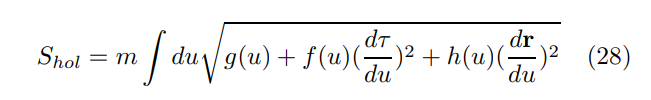
\ 通過對 τ(u) 和 r(u) 進行變分。
\ 在其測地線上評估此作用量,可得
\ 
\ 雖然(29)式的顯式解析計算只能在某些特殊情況下進行,但對於各種度量,單參數空間/時間依賴性可以很容易找到。具體來說,對於 HV 度量(26),可得[29, 30]
\ 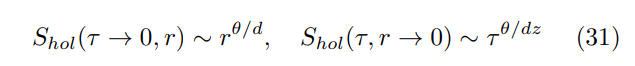
\ 值得注意的是,在沒有超尺度違規(θ = 0)的情況下,這兩種漸近行為要麼變為常數(可能性較小),要麼變為對數(可能性較大,見下文)。因此,如果經典 EMD 拉格朗日量(22)要代表具有類規範相互作用(1)的邊界理論的有效體積對偶,則漸近行為(31)將難以與主要依賴於 z(通過 η)而非 θ 的艾康納爾/玻色化結果(11,21)相協調。
\ 
\ 並由兩個獨立解組成,其形式為
\ 
\ 施加適當的邊界條件並遵循全息字典[26],然後將傳播子定義為入射在邊界的波的反射係數
\ 
\ 當 α = β + 1 時,會出現不同的行為(在有限 z 和 θ 的 HV 度量(26)情況下無法實現),此時(33)中的積分在 u → 0 處發散。這種特殊的非費米液體(NFL)區域,被稱為「局部臨界性」,其特徵是傳播子
\ 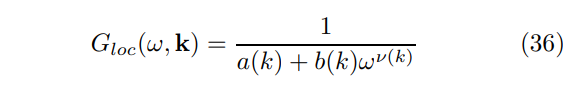
\ 其中 a(k)、b(k) 和 ν(k) ∼ k 是動量的非奇異函數,通常可以產生被識別為不同(「分數化」)費米面(FS)[28]的多個極點。
\ 對(36)進行傅立葉變換的複雜性在於 G(ω, k) 在其參數的整個範圍內並不能解析地知道。然而,通過鞍點的快速(和/或猛烈)傅立葉變換表明,這個函數在時空域中的形式如下
\ 
\ 更加引人入勝的是,最近對二維哈伯德和 t − J 模型的蒙特卡羅結果,這些模型長期以來被認為代表銅酸鹽中的原型非費米液體正常態。這些結果並不容易符合動量獨立但能量強依賴的自能函數,顯示出比上述任何表達式更少的能量/溫度依賴性[33]。這對於由相互作用(1)支配的費米子(「自旋子」)理論在分析這些微觀模型中的普遍適用性意味著什麼,仍有待觀察。
\
:::info 作者:
(1) D. V. Khveshchenko,北卡羅來納大學教堂山分校物理與天文學系,NC 27599。
:::
:::info 本論文可在 arxiv 上獲取,採用 CC BY 4.0 DEED 許可證。
:::
\
您可能也會喜歡

微軟認為 AI 差距正在擴大,儘管採用速度比任何其他技術都快

巴西的 OranjeBTC 加入struggling Crypto Treasury 公司轉向回購的浪潮

四年週期結論:2026年前加密貨幣的五大顛覆性趨勢
- DATs 2.0:Bitcoin金融服務將獲得合法性。 數位資產財庫公司今年經歷了快速擴張,但這也伴隨著成長的陣痛。從風味飲料到防曬品牌,各種公司都在將自己重新包裝為加密貨幣的買家和持有者,這給這一模式帶來了問題,包括投資者懷疑、監管阻力、管理不善和低估值。在眾多公司湧現的同時,一些DATs也開始持有我們可能稱為「山寨幣」的資產,但實際上,大多數這些項目缺乏歷史表現或投資價值,僅是投機工具。然而,在來年,DAT市場及其運營策略中的許多問題將得到解決,那些基於Bitcoin標準運營的真正實體將在公開市場中找到自己的位置。許多DATs,甚至是最大的那些,將看到其股價開始更緊密地與其底層資產價值趨同。管理層將面臨更有效地為股東創造價值的壓力。眾所周知,一家僅持有大量Bitcoin而不做任何事情(同時維持私人飛機和高管理費等大額支出)的公司對股東不利。
- 穩定幣將無處不在。 2026年將是穩定幣廣泛採用的一年。USDC和USDT預計將超越交易和結算,更深入地滲透到傳統金融交易和產品中。穩定幣可能不僅出現在加密貨幣交易所,還會出現在支付處理器、企業財務管理系統,甚至跨境結算系統中。對企業而言,吸引力在於它們能夠實現即時結算,而不依賴緩慢或昂貴的傳統銀行渠道。然而,類似於DATs領域,穩定幣市場也可能經歷過度飽和:太多投機性穩定幣項目正在推出,太多面向消費者的支付平台和錢包正在湧現,太多區塊鏈聲稱「支持」穩定幣。到今年年底,我們預計許多高度投機的項目將被市場淘汰或收購,市場將在更知名的穩定幣發行商、零售商、支付渠道和交易所/錢包下整合。
- 我們將告別「四年週期」理論。 我現在正式預測,Bitcoin的「四年週期」理論將在2026年正式結束。市場現在更廣泛,機構參與度更高,不再在真空中運作。相反,新的市場結構和持續的購買力將推動Bitcoin走向持續、漸進的增長軌跡。這意味著整體波動性將降低,其作為價值儲存的功能將變得更加穩定,這應該會吸引全球更多傳統投資者和市場參與者。Bitcoin將從交易工具演變為新的資產類別,伴隨著更穩定的現金流、更長的持有期,以及整體上更少的所謂「週期」。
- 美國投資者將獲得進入離岸流動性市場的機會。 隨著數位資產變得更加主流,加上有利的政府政策,法規和市場結構的變化將允許美國投資者獲取海外加密貨幣流動性。這可能不是突然的轉變,但隨著時間推移,我們將看到更多獲批的附屬機構、更複雜的託管解決方案,以及能夠符合美國標準的離岸平台。某些穩定幣項目也可能加速這一趨勢。美元支持的穩定幣已經能夠以傳統銀行渠道無法實現的方式跨境流動。隨著主要發行商進入受監管的離岸市場,它們有望成為連接美國資本與全球流動性池的橋樑。簡而言之,穩定幣最終可能正是監管機構一直在努力解決的問題:以清晰且可追蹤的方式將美國投資者與國際數位資產市場連接起來。這一點至關重要,因為離岸流動性在數位資產市場的價格發現中發揮著關鍵作用。市場成熟的下一階段將是跨境市場運作的標準化。
- 產品將趨向更加複雜和精細。 在新的一年,與Bitcoin相關的債務和股權產品的複雜性,以及專注於Bitcoin計價回報的交易產品,將達到新的高度。投資者,包括那些以前迴避數位資產的人,將接受這種更新、更精細的投資組合。我們可能會看到使用Bitcoin作為抵押品的結構性產品,以及旨在從Bitcoin敞口產生實際回報的投資策略(而不僅僅是押注價格變動)。ETF也開始超越簡單的價格追蹤,通過質押或期權策略提供回報來源,儘管完全多元化的總回報產品仍然有限。衍生品將變得更加複雜,並更好地與標準風險框架整合。到2026年,Bitcoin的功能可能會從主要作為投機工具轉變為金融基礎設施的核心組成部分。